Ngân hàng bài tập
S
Một viên gạch hoa hình vuông cạnh \(40\) cm. Người ta đã dùng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (phần tô đậm như hình vẽ).
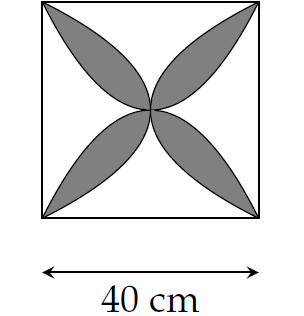
Diện tích của mỗi cánh hoa đó bằng
| \(200\) cm\(^2\) | |
| \(\dfrac{800}{3}\) cm\(^2\) | |
| \(\dfrac{400}{3}\) cm\(^2\) | |
| \(\dfrac{200}{3}\) cm\(^2\) |
1 lời giải
Chọn phương án C.
Đặt hình vuông vào hệ trục tọa độ \(Oxy\) như hình vẽ, cạnh của hình vuông ta có thể coi có độ dài bằng \(2\) trên hệ trục tọa độ.

Khi đó diện tích một cánh hoa chính là diện tích hình phẳng giới hạn bởi hai đồ thị \(y=x^2\) và \(y=\sqrt{x}\). Ta có
$$\begin{aligned}S_1&=\displaystyle\int\limits_0^1\left(\sqrt{x}-x^2\right)\mathrm{\,d}x\\
&=\left(\dfrac{2}{3}x\sqrt{x}-\dfrac{x^3}{3}\right)\bigg|_0^1\\
&=\dfrac{1}{3}.\end{aligned}$$
Vậy thực tế diện tích của mỗi cánh hoa là
$$S=20\times 20\times S_1=\dfrac{400}{3} \text{cm}^2.$$

