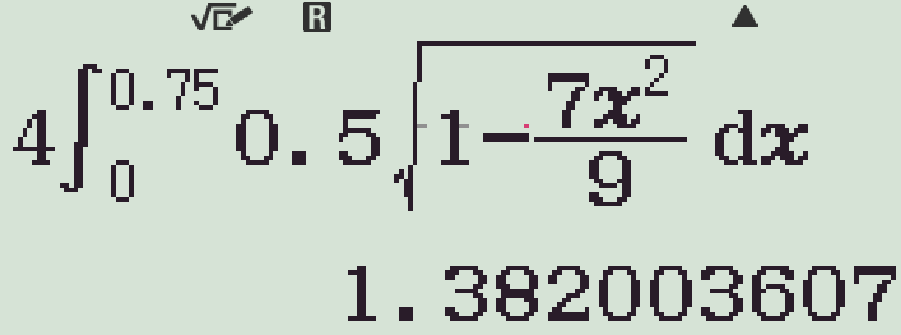Một quán cà phê muốn làm cái bảng hiệu là một phần của Elip có kích thước, hình dạng giống như hình vẽ và có chất lượng bằng gỗ.
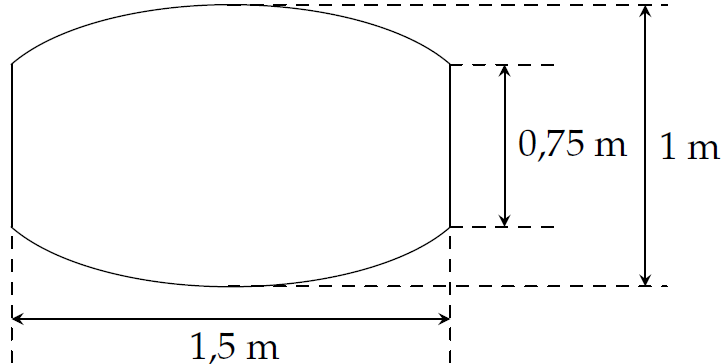
Diện tích gỗ bề mặt bẳng hiệu làm tròn đến hàng phần chục là
| \(1,4\) | |
| \(1,3\) | |
| \(1,5\) | |
| \(1,6\) |
Chọn phương án A.
Đặt hệ trục tọa độ như hình vẽ.
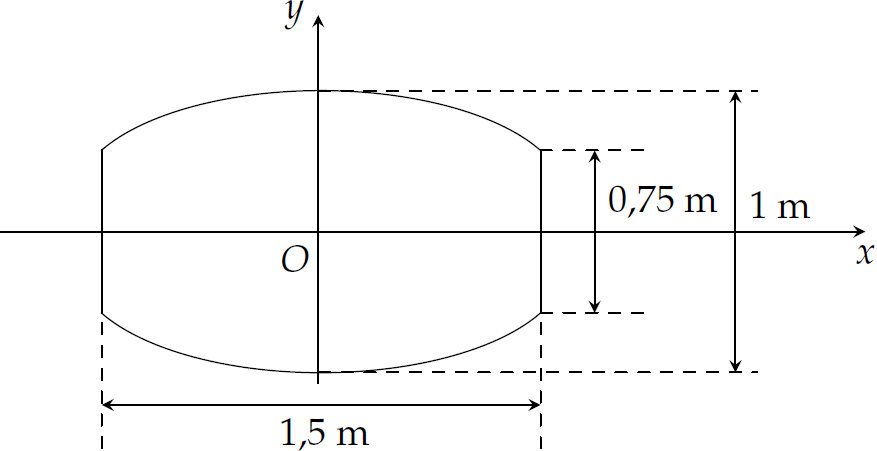
Gọi phương trình Elip cần tìm là $$(E)\colon\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.$$
Từ hình vẽ ta thấy \(b=0,5\) và \(M(0,75;0,375)\) là một điểm thuộc \((E)\), suy ra $$\dfrac{0,75^2}{a^2}+\dfrac{0,375^2}{0{,}5^2}=1\Rightarrow a^2=\dfrac{9}{7}.$$
Phương trình \((E)\colon \dfrac{7x^2}{9}+\dfrac{y^2}{0{,}5^2}=1\).
Trong góc phần tư thứ nhất: \(y=0,5\sqrt{1-\dfrac{7x^2}{9}}\).
Diện tích của bảng hiệu bằng \(4\) lần diện tích tấm bảng trong góc phần tư thứ nhất nên $$S=4\displaystyle\int\limits_{0}^{0,75}0,5\sqrt{1-\dfrac{7x^2}{9}} \mathrm{\,d}x\approx1,4.$$