Ngân hàng bài tập
S
Cho tam giác \(ABC\) có diện tích \(S\). Gọi \(M,\,N\) là hai điểm thỏa mãn \(\overrightarrow{AM}=2\overrightarrow{AB}\), \(\overrightarrow{CN}=-2\overrightarrow{AC}\). Tính diện tích \(\Delta AMN\) theo \(S\).
| \(2S\) | |
| \(8S\) | |
| \(4S\) | |
| \(6S\) |
1 lời giải
Chọn phương án A.
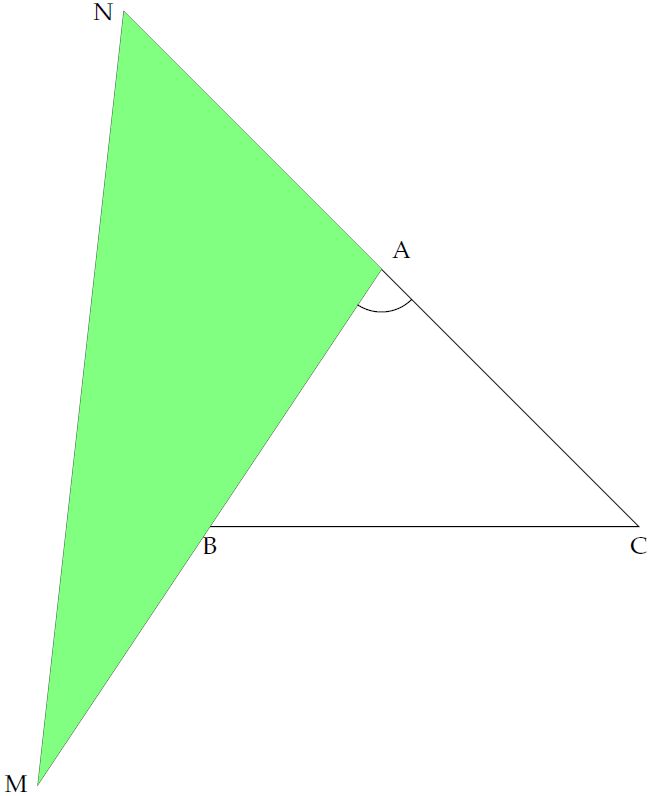
Theo đề bài ta có
- \(S=\dfrac{1}{2}AB\cdot AC\sin\widehat{BAC}\)
- \(AM=2AB\), \(AN=AC\)
- \(\widehat{BAC}\) và \(\widehat{MAN}\) là hai góc kề bù, tức là $$\sin\widehat{BAC}=\sin\widehat{MAN}$$
Do đó diện tích tam giác \(AMN\) bằng $$\begin{align*}\dfrac{1}{2}AM\cdot AN\sin\widehat{MAN}&=\dfrac{1}{2}2AB\cdot AC\sin\widehat{BAC}\\
&=2\left(\dfrac{1}{2}AB\cdot AC\sin\widehat{BAC}\right)\\
&=2S.\end{align*}$$
