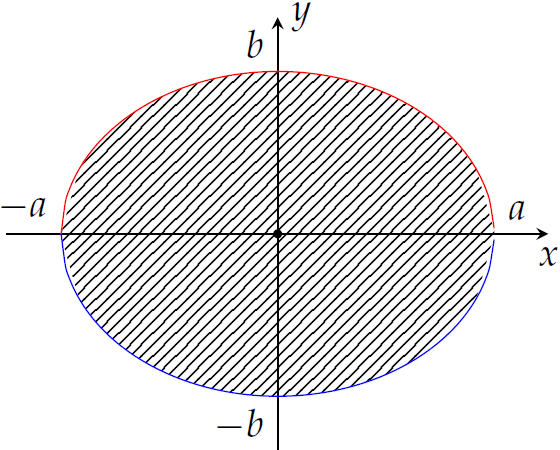
Tính diện tích \(S\) của hình phẳng giới hạn bởi elip \((E)\) có phương trình \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), với \(a,\,b>0\).
| \(S=\pi\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\) | |
| \(S=\pi(a+b)^2\) | |
| \(S=\pi ab\) | |
| \(S=\dfrac{\pi a^2b^2}{a+b}\) |
Chọn phương án C.
Từ phương trình của \((E)\) ta suy ra $$y=\pm b\sqrt{1-\dfrac{x^2}{a}}.$$
Khi đó, \(S=2\displaystyle\int\limits_{-a}^{a}b\sqrt{1-\dfrac{x^2}{a}}\mathrm{\,d}x\).
Đặt \(x=a\sin t\) \(\left(-\dfrac{\pi}{2}\leq t\leq\dfrac{\pi}{2}\right)\).
- \(\mathrm{d}x=a\cos t\mathrm{\,d}t\)
- \(x=a\Rightarrow t=\dfrac{\pi}{2}\)
- \(x=-a\Rightarrow t=-\dfrac{\pi}{2}\)
Khi đó: $$\begin{eqnarray*}
S&=&2\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}b\sqrt{1-\dfrac{a^2\sin^2t}{a^2}}\cdot a\cos t\mathrm{\,d}t\\
&=&2ab\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\sqrt{1-\sin^2t}\cdot\cos t\mathrm{\,d}t\\
&=&2ab\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\cos^2t\mathrm{\,d}t\\
&=&2ab\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\dfrac{1+\cos2t}{2}\mathrm{\,d}t\\
&=&ab\left(t+\dfrac{\sin2t}{2}\right)\bigg|_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\\
&=&\pi ab.
\end{eqnarray*}$$
