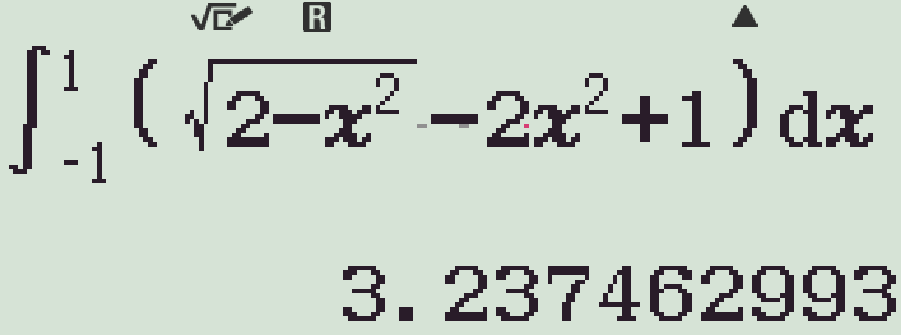Cho \((H)\) là hình phẳng giới hạn bởi parabol \(y=2x^2-1\) và nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) với \(-\sqrt{2}\leq x\leq\sqrt{2}\) (phần gạch chéo trong hình vẽ).
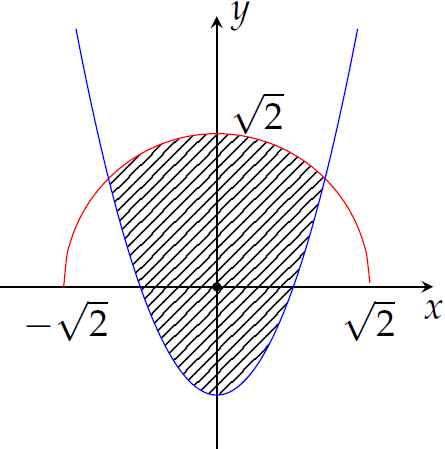
Diện tích của hình \((H)\) bằng
| \(\dfrac{3\pi-2}{6}\) | |
| \(\dfrac{3\pi+10}{3}\) | |
| \(\dfrac{3\pi+2}{6}\) | |
| \(\dfrac{3\pi+10}{6}\) |
Chọn phương án D.
Phương trình hoành độ giao điểm: $$\begin{aligned}
\sqrt{2-x^2}=2x^2-1\Leftrightarrow&\begin{cases}
2x^2-1\geq0\\ 2-x^2=4x^4-4x^2+1
\end{cases}\\
\Leftrightarrow&\begin{cases}
2x^2-1\geq0\\ 4x^4-3x^2-1=0
\end{cases}\\
\Leftrightarrow&\begin{cases}
2x^2-1\geq0\\ \left[\begin{array}{ll}
x=-1 &\text{(nhận)}\\ x=1 &\text{(nhận)}
\end{array}\right.
\end{cases}\\
\end{aligned}$$
Khi đó: $$\begin{eqnarray*}
S&=&\int\limits_{-1}^1\left(\sqrt{2-x^2}-2x^2+1\right)\mathrm{d}x\\
&=&\int\limits_{-1}^1\sqrt{2-x^2}\mathrm{d}x+\left(-\dfrac{2x^3}{3}+x\right)\bigg|_{-1}^1\\
&=&\int\limits_{-1}^1\sqrt{2-x^2}\mathrm{d}x+\dfrac{2}{3}.
\end{eqnarray*}$$
- \(\mathrm{\,d}x=\sqrt{2}\cos t\mathrm{\,d}t\)
- \(x=1\Rightarrow t=\dfrac{\pi}{4}\)
- \(x=-1\Rightarrow t=-\dfrac{\pi}{4}\)
Suy ra $$\begin{eqnarray*}
\int\limits_{-1}^1\sqrt{2-x^2}\mathrm{d}x&=&\int\limits_{-\tfrac{\pi}{4}}^{\tfrac{\pi}{4}}\sqrt{2-2\sin^2t}\cdot\sqrt{2}\cos t\mathrm{d}t\\
&=&\sqrt{2}\int\limits_{-\tfrac{\pi}{4}}^{\tfrac{\pi}{4}}\sqrt{2\cos^2t}\cdot\cos t\mathrm{d}t\\
&=&2\int\limits_{-\tfrac{\pi}{4}}^{\tfrac{\pi}{4}}\cos^2t\mathrm{d}t\\
&=&2\int\limits_{-\tfrac{\pi}{4}}^{\tfrac{\pi}{4}}\dfrac{1+\cos2t}{2}\mathrm{d}t\\
&=&\left(t+\dfrac{\sin2t}{2}\right)\bigg|_{-\tfrac{\pi}{4}}^{\tfrac{\pi}{4}}\\
&=&\dfrac{\pi}{2}+1.
\end{eqnarray*}$$
Vậy \(S=\dfrac{\pi}{2}+1+\dfrac{2}{3}=\dfrac{3\pi+10}{6}\).