Cho hình phẳng trong hình vẽ bên (phần tô đậm) quay quanh trục hoành.

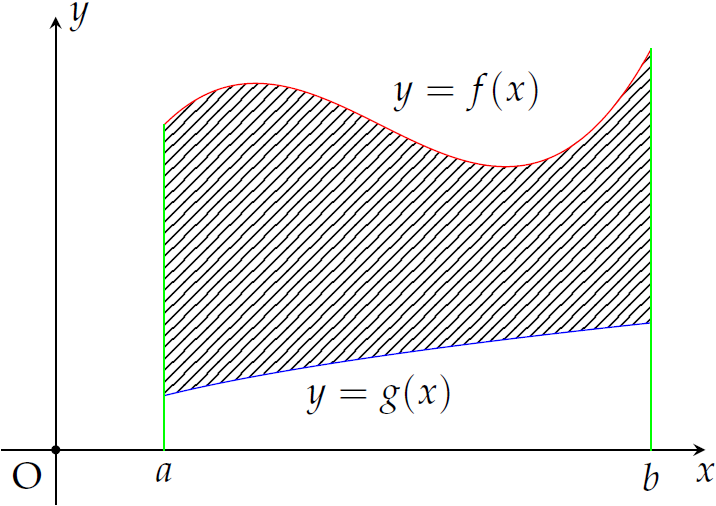
Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công thức sau đây?

	\(V=\pi\displaystyle\int\limits_{a}^{b}\left[g^2(x)-f^2(x)\right]\mathrm{\,d}x\)
	\(V=\pi\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]^2\mathrm{\,d}x\)
	\(V=\pi\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]\mathrm{\,d}x\)
	\(V=\pi\displaystyle\int\limits_{a}^{b}\left[f^2(x)-g^2(x)\right]\mathrm{\,d}x\)