Ngân hàng bài tập
B
Hàm số \(y=-x^3-3x^2+9x+20\) đồng biến trên khoảng nào sau đây?
| \((3;+\infty)\) | |
| \((1;2)\) | |
| \((-\infty;1)\) | |
| \((-3;1)\) |
1 lời giải
Chọn phương án D.
Tập xác định: \(\mathscr{D}=\mathbb{R}\).
Ta có: \(y'=-3x^2-6x+9\).
Cho \(y'=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=-3.\end{array}\right.\)
Bảng biến thiên: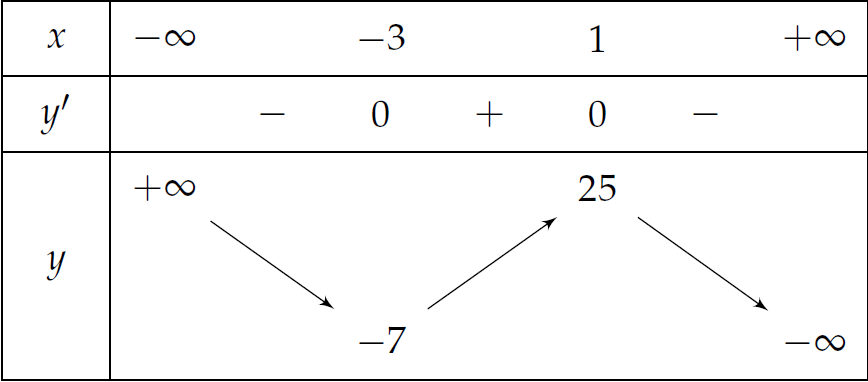
Vậy hàm số đồng biến trên khoảng \((-3;1)\).
