Ngân hàng bài tập
S
Tìm tất cả các giá trị thực của tham số \(m\) sao cho hàm số $$y=x^4-2(m-1)x^2+m-2$$đồng biến trên khoảng \((1;3)\).
| \(m\in(-\infty;-5)\) | |
| \(m\in[-5;2)\) | |
| \(m\in(2;+\infty)\) | |
| \(m\in(-\infty;2]\) |
1 lời giải
Chọn phương án D.
Tập xác định: \(\mathscr{D}=\mathbb{R}\).
Ta có: $$y'=4x^3-4(m-1)x=4x\left[x^2-m+1\right].$$
- Trường hợp \(m\leq1\):
Ta có \(y'=0\Leftrightarrow x=0\).
Bảng biến thiên: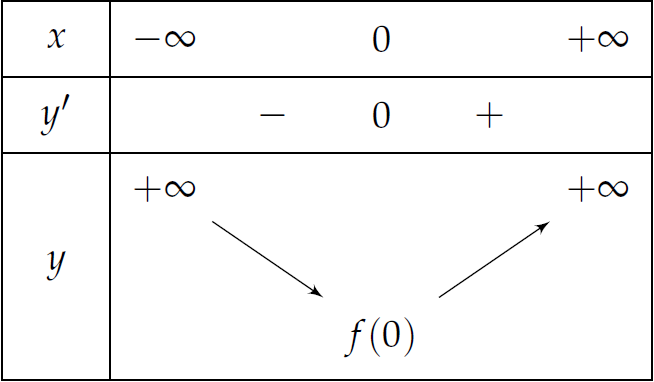 Khi đó, hàm số đồng biến trên \((0;+\infty)\) nên cũng đồng biến trên \((1;3)\) (1).
Khi đó, hàm số đồng biến trên \((0;+\infty)\) nên cũng đồng biến trên \((1;3)\) (1). - Trường hợp \(m>1\):
Ta có \(y'=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=\pm\sqrt{m-1}\end{array}\right.\)
Bảng biến thiên: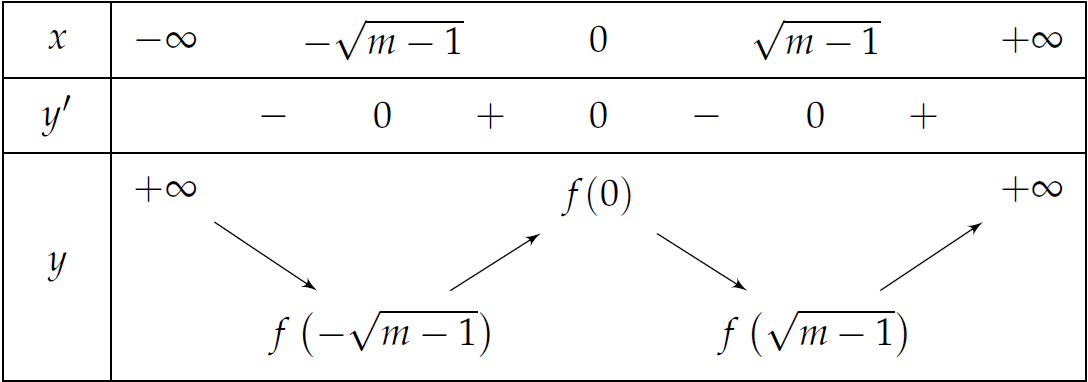 Khi đó, hàm số đồng biến trên \((1;3)\) khi \(\sqrt{m-1}\leq1\Leftrightarrow m\leq2\), tức là \(1<m\leq2\) (2).
Khi đó, hàm số đồng biến trên \((1;3)\) khi \(\sqrt{m-1}\leq1\Leftrightarrow m\leq2\), tức là \(1<m\leq2\) (2).
Từ (1) và (2) suy ra \(m\in(-\infty;1]\cup(1;2]\), hay \(m\in(-\infty;2]\).
