Ngân hàng bài tập
S
Tìm tất cả các giá trị của tham số \(m\) để hàm số $$y=(m-1)x^3+(m-1)x^2-(2m+1)x+5$$nghịch biến trên tập xác định.
| \(-\dfrac{5}{4}\leq m\leq1\) | |
| \(-\dfrac{2}{7}\leq m<1\) | |
| \(-\dfrac{7}{2}\leq m<1\) | |
| \(-\dfrac{2}{7}\leq m\leq1\) |
1 lời giải
Chọn phương án D.
Tập xác định: \(\mathscr{D}=\mathbb{R}\).
Ta có \(y'=3(m-1)x^2+2(m-1)x-(2m+1)\).
- Trường hợp \(m=1\):
\(y'=-(2\cdot1+1)=-3<0,\;\forall x\in\mathbb{R}\) nên hàm số nghịch biến trên tập xác định (1). - Trường hợp \(m\neq1\):
Hàm số nghịch biến trên \(\mathbb{R}\) khi $$\begin{aligned}y'\leq0,\;\forall x\in\mathbb{R}\Leftrightarrow&\,\begin{cases}a<0\\ \Delta'\leq0\end{cases}\\ \Leftrightarrow&\,\begin{cases}m-1<0\\ (m-1)^2+3(m-1)(2m+1)\leq0\end{cases}\\ \Leftrightarrow&\,\begin{cases}m<1\\ 7m^2-5m-2\leq0\end{cases}\end{aligned}$$Xét dấu \(\Delta'\):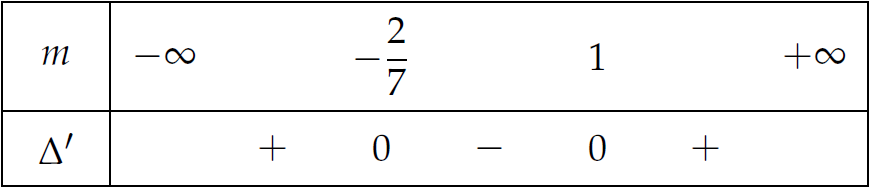 Vậy \(\begin{cases}m<1\\ -\dfrac{2}{7}\leq m\leq1\end{cases}\Leftrightarrow-\dfrac{2}{7}\leq m<1\) (2).
Vậy \(\begin{cases}m<1\\ -\dfrac{2}{7}\leq m\leq1\end{cases}\Leftrightarrow-\dfrac{2}{7}\leq m<1\) (2).
Từ (1) và (2) suy ra \(-\dfrac{2}{7}\leq m\leq1\).
