Ngân hàng bài tập
B
Cho hàm số \(y=f(x)\) thỏa mãn \(f'(x)=x^2-5x+4,\;\forall x\in\mathbb{R}\). Khẳng định nào sau đây là đúng?
| Hàm số đồng biến trên khoảng \((-\infty;3)\) | |
| Hàm số nghịch biến trên khoảng \((3;+\infty)\) | |
| Hàm số nghịch biến trên khoảng \((2;3)\) | |
| Hàm số đồng biến trên khoảng \((1;4)\) |
1 lời giải
Chọn phương án C.
Cho \(f'(x)=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=4\end{array}\right.\)
Bảng biến thiên: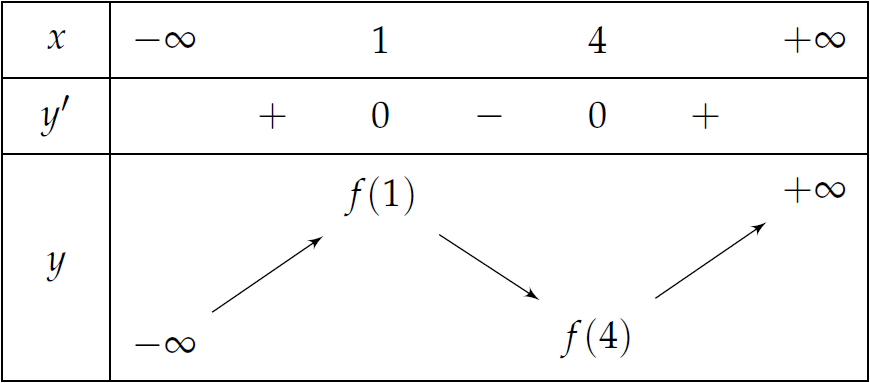
Vậy hàm số đã cho nghịch biến trên khoảng \((1;4)\) nên cũng nghịch biến trên khoảng \((2;3)\).
