Ngân hàng bài tập
A
Cho số phức \(z\) thỏa mãn \(z(1+3i)=17+i\). Khi đó môđun của số phức \(w=6\overline{z}-25i\) là
| \(\sqrt{29}\) | |
| \(13\) | |
| \(2\sqrt{5}\) | |
| \(5\) |
2 lời giải
Chọn phương án B.
Dùng máy tính cầm tay:
- Lưu \(z=\dfrac{17+\mathrm{i}}{1+3\mathrm{i}}\) vào biến nhớ A

- Nhập q(6T2Qz)p25b=
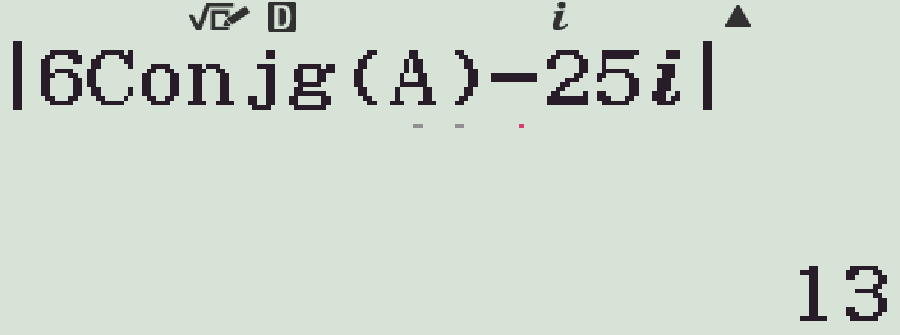
Chọn phương án B.
Ta có \(z=\dfrac{17+i}{1+3i}=2+5i\).
Khi đó, \(w=6(2+5i)-25i=12+5i\).
Suy ra \(|w|=\sqrt{12^2+5^2}=13\).
