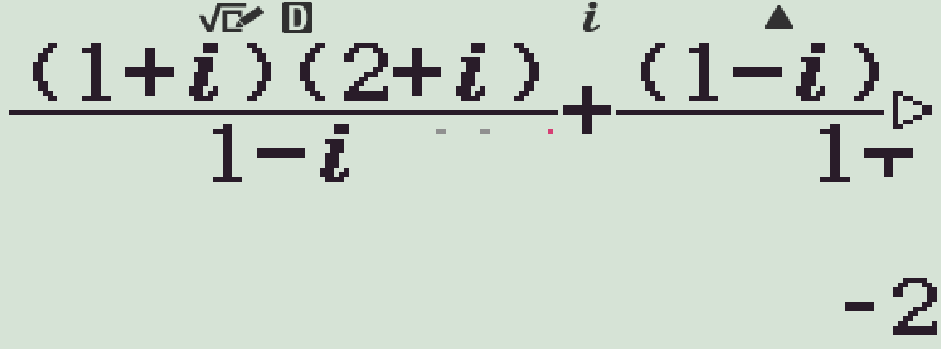Ngân hàng bài tập
B
Cho số phức \(z\) thỏa mãn $$z=\dfrac{(1+i)(2+i)}{1-i}+\dfrac{(1-i)(2-i)}{1+i}.$$Trong các kết luận sau, kết luận nào đúng?
| \(z=\overline{z}\) | |
| \(z\) là số thuần ảo | |
| \(|z|=4\) | |
| \(z=\dfrac{1}{\overline{z}}\) |
1 lời giải
Chọn phương án A.
\(\begin{aligned}
z&=\dfrac{1+3i}{1-i}+\dfrac{1-3i}{1+i}\\
&=\dfrac{(1+3i)(1+i)}{2}+\dfrac{(1-3i)(1-i)}{2}\\
&=\dfrac{-2+4i}{2}+\dfrac{-2-4i}{2}\\
&=-2.
\end{aligned}\)
Khi đó, \(\overline{z}=-2=z\).