Ngân hàng bài tập
A
Cho số phức \(z\) thỏa mãn $$\overline{z}=\dfrac{4(-3+i)}{1-2i}+\dfrac{(3-i)^2}{-i}$$Môđun của số phức \(w=z-i\overline{z}+1\) là
| \(|w|=\sqrt{85}\) | |
| \(|w|=4\sqrt{5}\) | |
| \(|w|=6\sqrt{3}\) | |
| \(|w|=\sqrt{48}\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Nhập \(\dfrac{4(-3+i)}{1-2i}+\dfrac{(3-i)^2}{-i}\)=
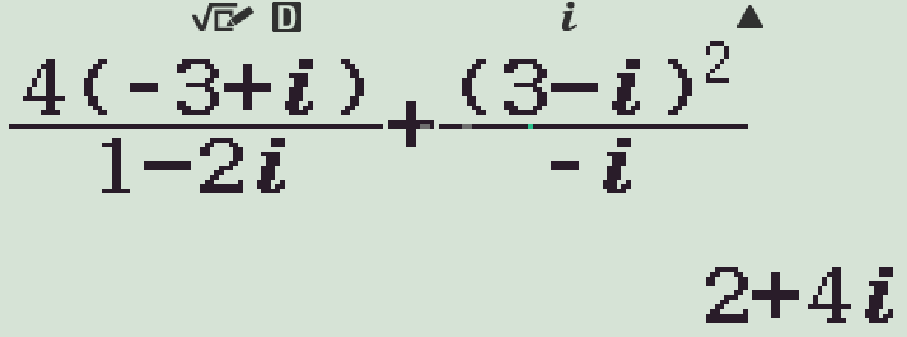
Lúc này, \(\overline{z}\) đã được lưu vào biến M. - Nhập T2M)pbM+1=
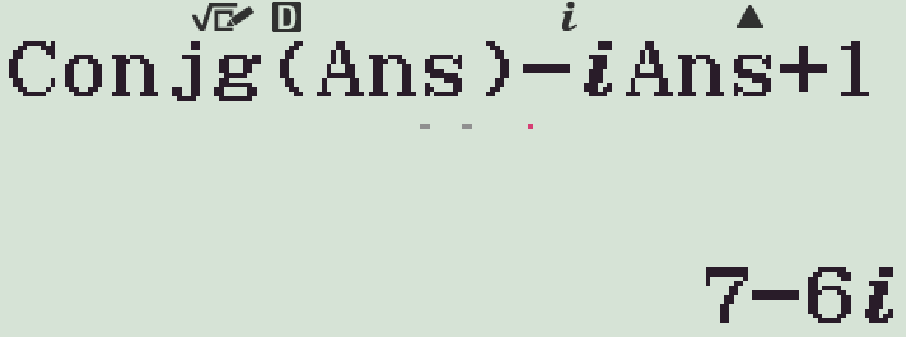
- Nhập q(M=

Chọn phương án A.
\(\begin{aligned}
\overline{z}&=\dfrac{4(-3+i)}{1-2i}+\dfrac{(3-i)^2}{-i}\\
&=2+4i\\
\Rightarrow z&=2-4i.
\end{aligned}\)
Khi đó:$$\begin{aligned}
w&=z-i\overline{z}+1\\
&=(2-4i)-i(2+4i)+1\\
&=7-6i.\\
\Rightarrow|w|&=\sqrt{7^2+(-6)^2}=\sqrt{85}.
\end{aligned}$$
