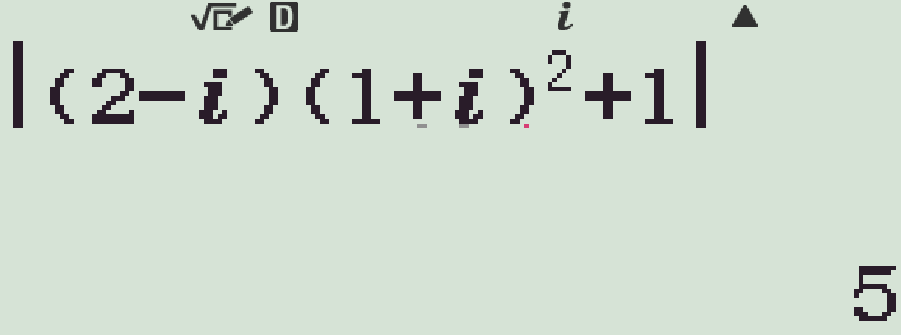Ngân hàng bài tập
C
Tính môđun của số phức $$z=(2-\mathrm{i})(1+\mathrm{i})^2+1$$
| \(|z|=4\) | |
| \(|z|=5\) | |
| \(|z|=2\sqrt{5}\) | |
| \(|z|=25\) |
1 lời giải
Chọn phương án B.
Ta có \((1+\mathrm{i})^2=2\mathrm{i}\).
Khi đó \(z=(2-\mathrm{i})2\mathrm{i}+1=3+4\mathrm{i}\).
Suy ra \(|z|=\sqrt{3^2+4^2}=5\).