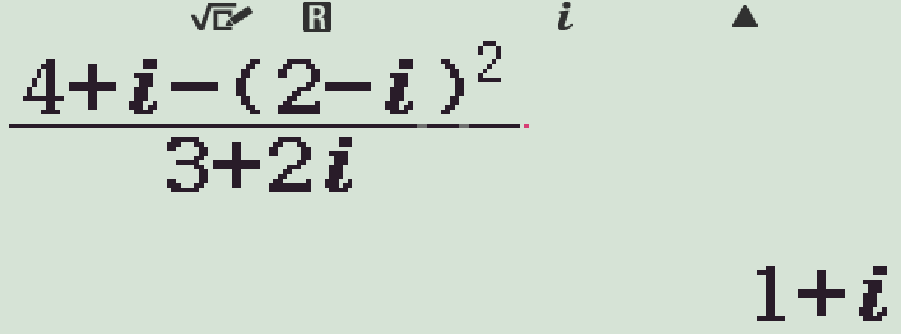Ngân hàng bài tập
A
Cho số phức \(z\) thỏa mãn $$(3+2\mathrm{i})z+(2-\mathrm{i})^2=4+\mathrm{i}$$Hiệu phần thực và phần ảo của \(z\) là
| \(2\) | |
| \(3\) | |
| \(1\) | |
| \(0\) |
1 lời giải
Chọn phương án D.
\(\begin{aligned}
(3+2\mathrm{i})z+(2-\mathrm{i})^2&=4+\mathrm{i}\\
\Rightarrow z&=\dfrac{4+\mathrm{i}-(2-\mathrm{i})^2}{3+2\mathrm{i}}\\
&=1+\mathrm{i}.
\end{aligned}\)
Khi đó, hiệu phần thực và phần ảo của \(z\) là \(1-1=0\).