Ngân hàng bài tập
SS
Tìm các giá trị của \(m\) để phương trình \(9^x+6^x-m\cdot4^x=0\) có nghiệm.
| \(m>0\) | |
| \(m\leq0\) | |
| \(m<0\) | |
| \(m\geq0\) |
1 lời giải
Chọn phương án A.
\(\begin{aligned}
9^x+6^x-m\cdot4^x=0\Leftrightarrow&\,\dfrac{9^x}{4^x}+\dfrac{6^x}{4^x}-m=0\\
\Leftrightarrow&\,\left(\dfrac{3}{2}\right)^{2x}+\left(\dfrac{3}{2}\right)^x=m\quad(1)
\end{aligned}\)
Đặt \(t=\left(\dfrac{3}{2}\right)^x\) (\(t>0\)), phương trình (1) trở thành $$t^2+t-m=0\Leftrightarrow t^2+t=m$$
Đặt \(f(t)=t^2+t\), ta có:
- \(f(t)\) xác định trên \(\mathscr{D}=(0;+\infty)\)
- \(f'(t)=2t+1>0\) với \(\forall t\in\mathscr{D}\)
Bảng biến thiên: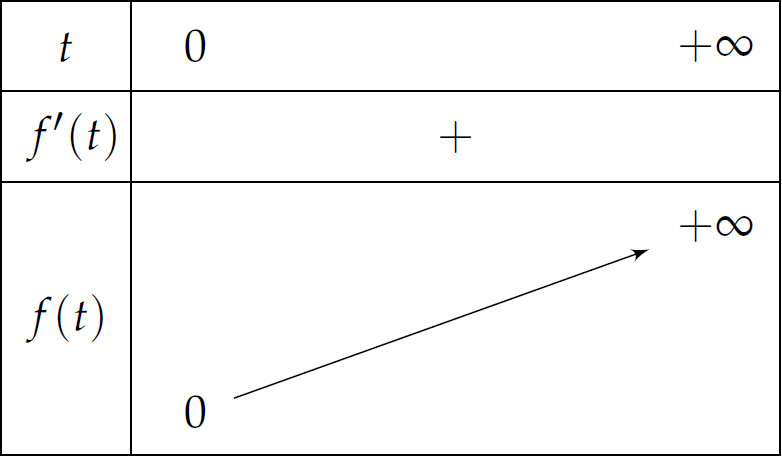
Vậy để phương trình đã cho có nghiệm thì \(m>0\).
