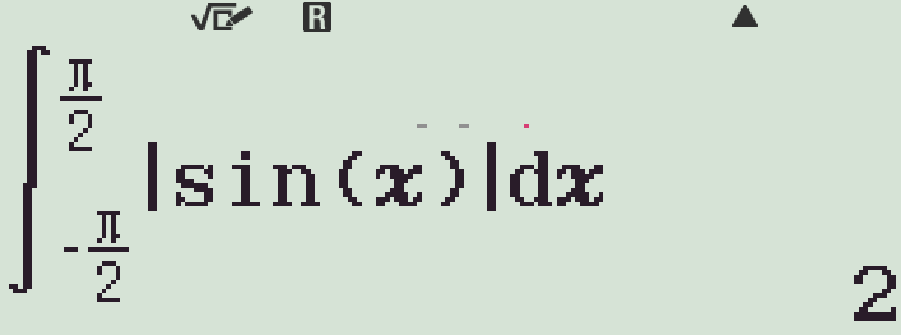Ngân hàng bài tập
C
Đặt \(\displaystyle I=\int\limits_{\tfrac{-\pi}{2}}^{\tfrac{\pi}{2}} \left|\sin x\right|\mathrm{\,d}x\). Khi đó
| \(I=\dfrac{1}{2}\) | |
| \(I=1\) | |
| \(I=0\) | |
| \(I=2\) |
1 lời giải
Chọn phương án D.
Vì \(\left|\sin x\right|=\begin{cases}\sin x &\text{khi }x\in\left[0;\dfrac{\pi}{2}\right]\\ -\sin x &\text{khi }x\in\left[-\dfrac{\pi}{2};0\right]\end{cases}\)
Nên ta có $$\begin{align*}
I&=\int\limits_{\tfrac{-\pi}{2}}^{\tfrac{\pi}{2}} \left|\sin x\right|\mathrm{\,d}x\\
&=\int\limits_{\tfrac{-\pi}{2}}^{0} -\sin x\mathrm{\,d}x+\int\limits_0^{\tfrac{\pi}{2}} \sin x\mathrm{\,d}x\\
&=\cos x\Big|_{\tfrac{-\pi}{2}}^0 -\cos x\Big|_0^{\tfrac{\pi}{2}}\\
&=2.\end{align*}$$