Ngân hàng bài tập
A
Tìm tập nghiệm của bất phương trình $$\log_{\tfrac{1}{2}}\left(x^2-5x+7\right)>0$$
| \((-\infty;2)\cup(3;+\infty)\) | |
| \((3;+\infty)\) | |
| \((-\infty;2)\) | |
| \((2;3)\) |
1 lời giải
Chọn phương án D.
Ta có \(x^2-5x+7=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}>0\), \(\forall x\in\mathbb{R}\).
Khi đó $$\begin{aligned}
&\,\log_{\tfrac{1}{2}}\left(x^2-5x+7\right)>0\\
\Leftrightarrow&\,\log_{\tfrac{1}{2}}\left(x^2-5x+7\right)>\log_{\tfrac{1}{2}}1\\
\Leftrightarrow&\,x^2-5x+7<1\\
\Leftrightarrow&\,x^2-5x+6<0.
\end{aligned}$$
Bảng xét dấu: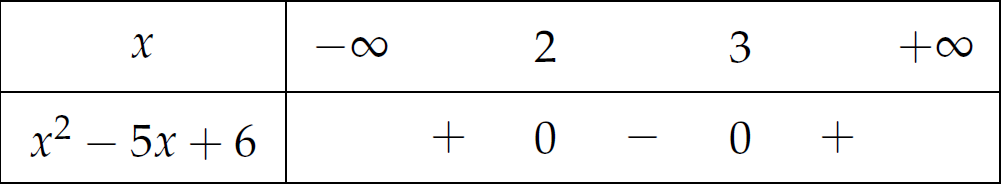
Vậy tập nghiệm của bất phương trình là \((2;3)\).
