Ngân hàng bài tập
A
Tìm tập nghiệm \(S\) của bất phương trình $$\left(\dfrac{1}{2}\right)^{-x^2+3x}<\dfrac{1}{4}$$
| \(S=[1;2]\) | |
| \(S=(-\infty;1)\) | |
| \(S=(1;2)\) | |
| \(S=(2;+\infty)\) |
1 lời giải
Chọn phương án C.
\(\begin{aligned}
\left(\dfrac{1}{2}\right)^{-x^2+3x}<\dfrac{1}{4}\Leftrightarrow&\,\log_{\tfrac{1}{2}}\left(\dfrac{1}{2}\right)^{-x^2+3x}>\log_{\tfrac{1}{2}}\dfrac{1}{4}\\
\Leftrightarrow&\,-x^2+3x>2\\
\Leftrightarrow&\,-x^2+3x-2>0.
\end{aligned}\)
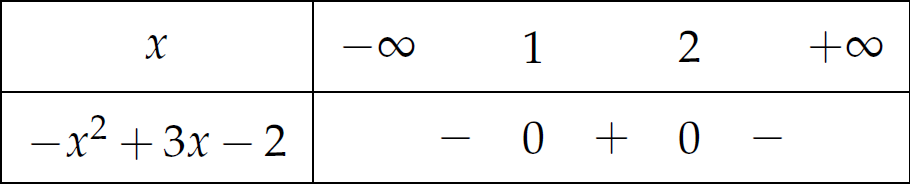
Vậy \(S=(1;2)\).
