Ngân hàng bài tập
S
Giải bất phương trình $$\left(10+3\sqrt{11}\right)^x+\left(10-3\sqrt{11}\right)^x\leq20$$
| \(0\leq x\leq1\) | |
| \(-1\leq x<1\) | |
| \(-1< x\leq1\) | |
| \(-1\leq x\leq1\) |
1 lời giải
Chọn phương án D.
Đặt \(t=\left(10+3\sqrt{11}\right)^x\;(t>0)\).
Ta thấy \(\left(10+3\sqrt{11}\right)\cdot\left(10-3\sqrt{11}\right)=1\).
Suy ra \(\left(10-3\sqrt{11}\right)^x=\dfrac{1}{t}\).
Do đó, phương trình đã cho trở thành $$t+\dfrac{1}{t}\leq20\Leftrightarrow\,t^2-20t+1\leq0$$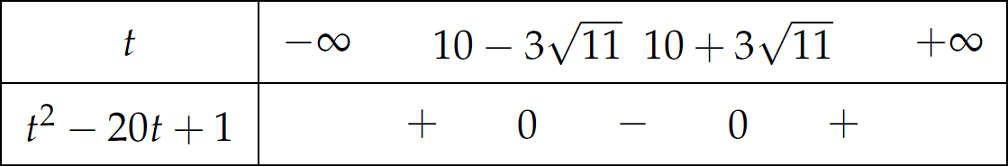
Suy ra $$\begin{aligned}
\begin{cases}
t\geq10-3\sqrt{11}\\
t\leq10+3\sqrt{11}
\end{cases}\Leftrightarrow&\begin{cases}
\left(10+3\sqrt{11}\right)^x\geq10-3\sqrt{11}\\
\left(10+3\sqrt{11}\right)^x\leq10+3\sqrt{11}
\end{cases}\\
\Leftrightarrow&\begin{cases}
x\geq-1\\
x\leq1.
\end{cases}
\end{aligned}$$
Vậy \(-1\leq x\leq1\).
