Ngân hàng bài tập
A
Tìm tập nghiệm của bất phương trình $$\log_{\sqrt{2}}(x+3)-\log_2x\leq4$$
| \(S=[1;+\infty)\) | |
| \(S=[1;9]\) | |
| \(S=(-\infty;9]\) | |
| \(S=(0;9]\) |
1 lời giải
Chọn phương án B.
Điều kiện: \(\begin{cases}
x+3>0\\ x>0
\end{cases}\Leftrightarrow x>0\).
Ta có $$\begin{aligned}
&\,\log_{\sqrt{2}}(x+3)-\log_2x\leq4\\
\Leftrightarrow&\,\log_{\sqrt{2}}(x+3)\leq\log_2x+4\\
\Leftrightarrow&\,\log_{2^{\frac{1}{2}}}(x+3)\leq\log_2x+\log_22^4\\
\Leftrightarrow&\,2\log_{2}(x+3)\leq\log_216x\\
\Leftrightarrow&\,\log_{2}(x+3)^2\leq\log_216x\\
\Leftrightarrow&\,(x+3)^2\leq16x\\
\Leftrightarrow&\,x^2-10x+9\leq0.
\end{aligned}$$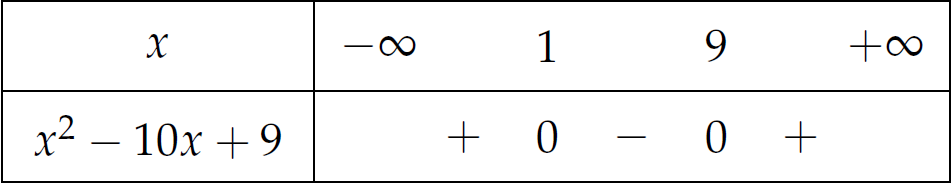
Suy ra \(x\in[1;9]\).
Vậy \(S=[1;9]\).
