Giải bất phương trình $$\log_x\left(\log_3\left(9^x-72\right)\right)\leq1$$
| \(S=(-\infty;2]\) | |
| \(S=\left(\log_3\sqrt{73};2\right]\) | |
| \(S=\left(\log_3\sqrt{72};2\right]\) | |
| \(S=\left[\log_3\sqrt{73};2\right]\) |
Chọn phương án B.
Điều kiện: $$\begin{aligned}
\begin{cases}
0< x\neq1\\
9^x-72>0\\
\log_3\left(9^x-72\right)>0
\end{cases}\Leftrightarrow&\begin{cases}
0< x\neq1\\
9^x>72\\
9^x-72>1
\end{cases}\\
\Leftrightarrow&\begin{cases}
0< x\neq1\\
9^x>73
\end{cases}\\
\Leftrightarrow&\,x>\log_973\\
\Leftrightarrow&\,x>\log_3\sqrt{73}\approx1,95\;(1)
\end{aligned}$$
Ta có $$\begin{aligned}
&\,\log_x\left(\log_3\left(9^x-72\right)\right)\leq1\\
\Leftrightarrow&\,x^{\log_x\left(\log_3\left(9^x-72\right)\right)}\leq x^1\\
\Leftrightarrow&\,\log_3\left(9^x-72\right)\leq x\\
\Leftrightarrow&\,3^{\log_3\left(9^x-72\right)}\leq3^x\\
\Leftrightarrow&\,9^x-72\leq3^x\\
\Leftrightarrow&\,\left(3^x\right)^2-3^x-72\leq0.
\end{aligned}$$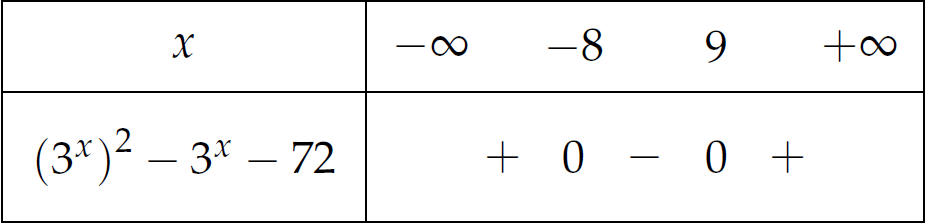
Vì \(3^x>0,\,\forall x\) nên suy ra $$3^x\leq9\Leftrightarrow x\leq2\;(2)$$
Từ (1) và (2) suy ra \(S=\left(\log_3\sqrt{73};2\right]\).
