Ngân hàng bài tập
A
Tìm số nghiệm nguyên của bất phương trình $$2\log_{\tfrac{1}{2}}|x-1|<\log_{\tfrac{1}{2}}x-1$$
| \(1\) | |
| \(3\) | |
| \(2\) | |
| Vô số |
1 lời giải
Chọn phương án D.
Điều kiện: \(\begin{cases}
|x-1|>0\\ x>0
\end{cases}\Leftrightarrow\begin{cases}
x\neq1\\ x>0.
\end{cases}\)
Ta có $$\begin{aligned}
&\,2\log_{\tfrac{1}{2}}|x-1|<\log_{\tfrac{1}{2}}x-1\\
\Leftrightarrow&\,\log_{\tfrac{1}{2}}|x-1|^2<\log_{\tfrac{1}{2}}x-\log_{\tfrac{1}{2}}\dfrac{1}{2}\\
\Leftrightarrow&\,\log_{\tfrac{1}{2}}(x-1)^2<\log_{\tfrac{1}{2}}(2x)\\
\Leftrightarrow&\,(x-1)^2>2x\\
\Leftrightarrow&\,x^2-4x+1>0.
\end{aligned}$$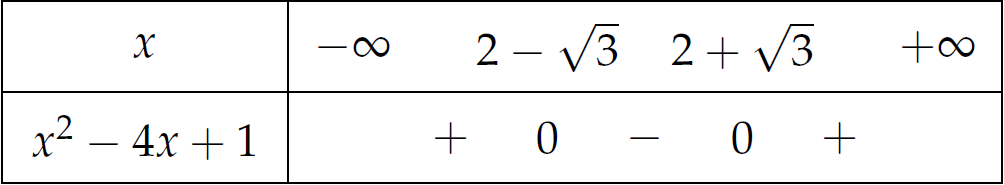
Suy ra \(x\in\left(-\infty;2-\sqrt{3}\right)\cup\left(2+\sqrt{3};+\infty\right)\).
Vì \(x\in\mathbb{Z}\) và \(0< x\neq1\) nên suy ra \(x\geq4\).
Vậy có vô số nghiệm nguyên thỏa đề.
