Ngân hàng bài tập
A
Tập nghiệm của bất phương trình \(\log_2^2x-3\log_2x+2<0\) là khoảng \((a;b)\). Tính \(a^2+b^2\).
| \(16\) | |
| \(5\) | |
| \(20\) | |
| \(10\) |
1 lời giải
Chọn phương án C.
Điều kiện: \(x>0\).
Đặt \(t=\log_2x\), ta có $$\log_2^2x-3\log_2x+2<0\Leftrightarrow t^2-3t+2<0$$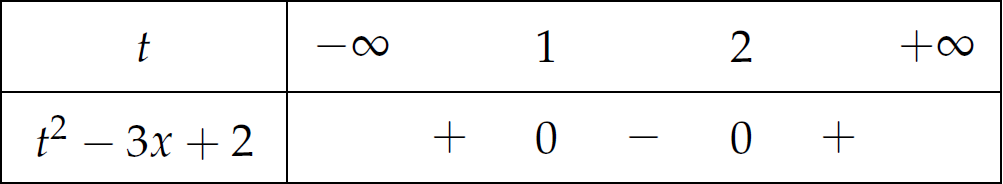
Suy ra $$\begin{aligned}
\begin{cases}
t>1\\ t<2
\end{cases}\Leftrightarrow&\begin{cases}
\log_2x>1\\ \log_2x<2
\end{cases}\\
\Leftrightarrow&\begin{cases}
x>2\\ x<4.
\end{cases}
\end{aligned}$$
Vậy tập nghiệm của bất phương trình đã cho là \((2;4)\).
Do đó \(\begin{cases}
a=2\\ b=4
\end{cases}\Rightarrow a^2+b^2=20\).
