Cho \(I=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\tan^2x\mathrm{\,d}x=a-\dfrac{b\pi}{c}\) với \(a\), \(b\), \(c\) là các số nguyên dương, \(b\) và \(c\) nguyên tố cùng nhau. Giá trị của biểu thức \(T=\dfrac{a}{b}+2c\) là
| \(7\) | |
| \(5\) | |
| \(9\) | |
| \(3\) |
Chọn phương án C.
Đặt $A=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\tan^2x\mathrm{\,d}x$, ta được $$A=a-\dfrac{b\pi}{c}\Leftrightarrow \dfrac{a-A}{\pi}=\dfrac{b}{c}$$Vì $a,\,b,\,c$ là các số nguyên dương nên ta dùng chức năng TABLE của máy tính cầm tay để khảo sát hàm số $f(x)=\dfrac{x-A}{\pi}$ và tìm giá trị $x$ sao cho $f(x)$ là số hữu tỉ.
- Lưu giá trị $\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\tan^2x\mathrm{\,d}x$ vào biến nhớ A
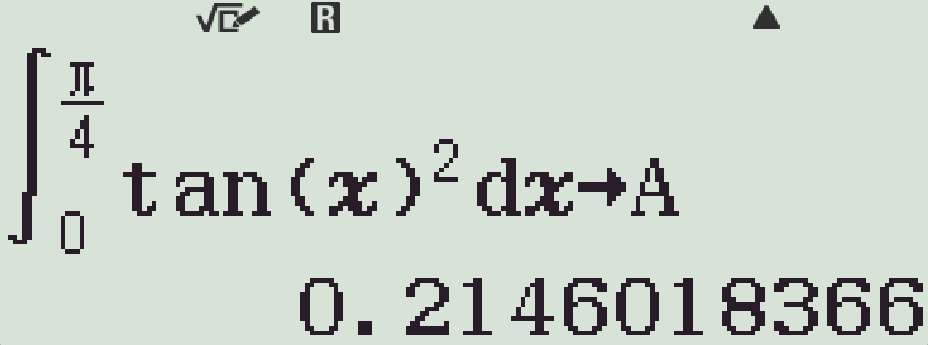
- Vào TABLE và nhập hàm số $f(x)=\dfrac{x-A}{\pi}$.

- Vì $a$ nguyên dương nên ta chọn Start=1, End=20 và Step=1.

- Ta tìm giá trị $x$ sao cho $f(x)$ là số hữu tỉ.

Vậy $a=1$ và $\dfrac{b}{c}=\dfrac{1}{4}$, tức là $b=1$ và $c=4$.
Do đó, $T=\dfrac{a}{b}+2c=9$.
Chọn phương án C.
\(\begin{align*}
I&=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\tan^2x\mathrm{\,d}x=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\left(\tan^2x+1-1\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\left(\dfrac{1}{\cos^2x}-1\right)\mathrm{\,d}x\\
&=\left(\tan x-x\right)\bigg|_0^{\tfrac{\pi}{4}}=1-\dfrac{\pi}{4}.\end{align*}\)
Do đó \(a=1\), \(b=1\), \(c=4\).
\(\Rightarrow T=\dfrac{a}{b}+2 c=9\).
