Ngân hàng bài tập
A
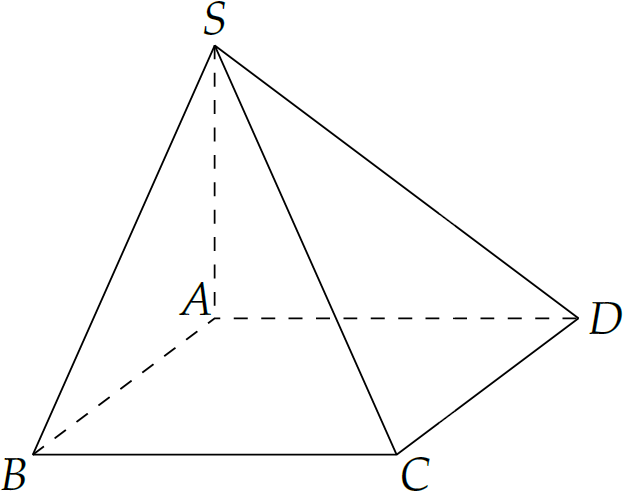
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\sqrt{3}\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=a\sqrt{2}\) (như hình minh họa trên). Góc giữa đường thẳng \(SC\) và mặt phẳng \((ABCD)\) bằng
| \(45^\circ\) | |
| \(30^\circ\) | |
| \(60^\circ\) | |
| \(90^\circ\) |
1 lời giải
Chọn phương án B.
Ta có: \(SA\bot\left(ABCD\right)\) nên \(AC\) là hình chiếu vuông góc của \(SC\) lên mặt phẳng \((ABCD)\).
Do đó, \(\left(SC,(ABCD)\right)=\left(SC,AC\right)=\widehat{SCA}\).
Xét \(\triangle SCA\) vuông tại A ta có $$\tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{2}}{a\sqrt{3}\cdot\sqrt{2}}=\dfrac{1}{\sqrt{3}}.$$
Suy ra \(\widehat{SCA}=30^\circ\).
