Ngân hàng bài tập
A
Cho hình nón có chiều cao bằng \(2\sqrt{5}\). Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng \(9\sqrt{3}\). Thể tích của khối nón giới hạn bởi hình nón đã cho bằng
| \(\dfrac{32\sqrt{5}\pi}{3}\) | |
| \(32\pi\) | |
| \(32\sqrt{5}\pi\) | |
| \(96\pi\) |
1 lời giải
Chọn phương án A.
Theo đề ta có:
- Chiều cao hình nón: \(h=2\sqrt{5}\).
- \(\triangle ABC\) đều có \(S_{ABC}=9\sqrt{3}\).
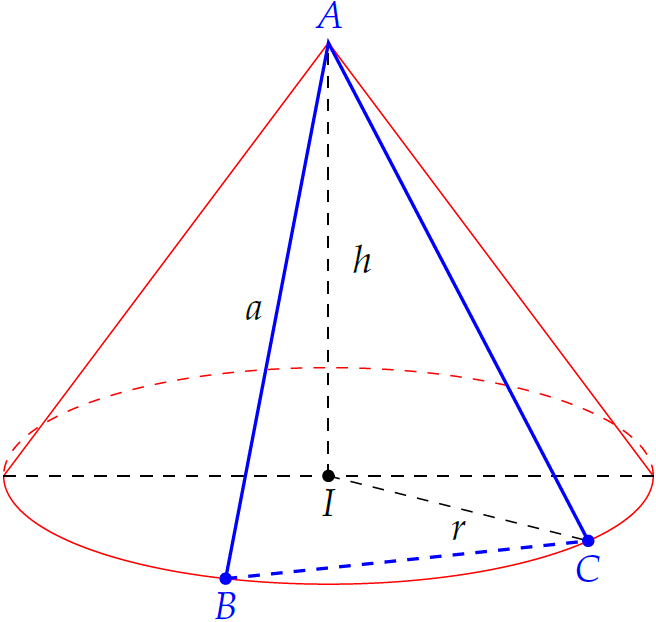
Giả sử \(\triangle ABC\) có cạnh bằng \(a\), khi đó $$\begin{aligned}
S_{ABC}=9\sqrt{3}\Leftrightarrow&\,\dfrac{a^2\sqrt{3}}{4}=9\sqrt{3}\\
\Leftrightarrow&\,a^2=36\\
\Leftrightarrow&\,a=6.
\end{aligned}$$
Khi đó, bán kính đáy của hình nón bằng $$r=\sqrt{6^2-\left(2\sqrt{5}\right)^2}=4.$$
Vậy thể tích khối nón đã cho bằng $$V=\dfrac{1}{3}\cdot\pi r^2\cdot h=\dfrac{32\pi\sqrt{5}}{3}.$$
