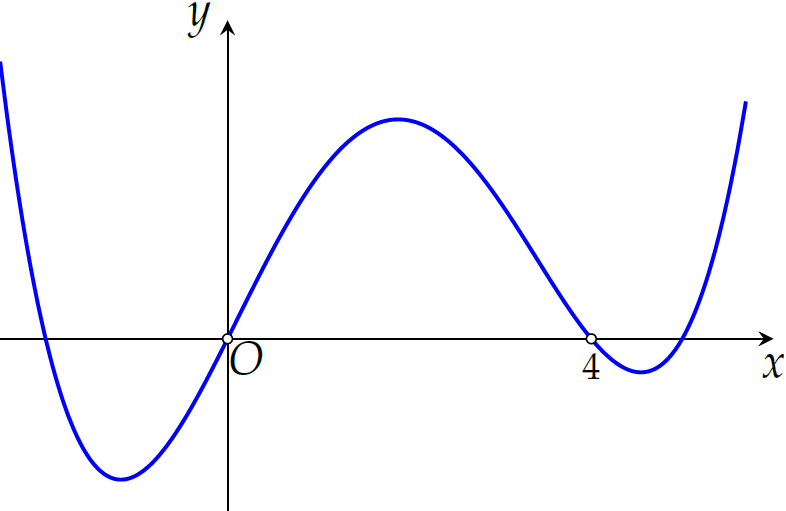
Cho hàm số bậc bốn \(y=f(x)\) có đồ thị như hình trên. Số điểm cực trị của hàm số \(g(x)=f\left(x^3+3x^2\right)\) là
| \(5\) | |
| \(3\) | |
| \(7\) | |
| \(11\) |
Chọn phương án C.
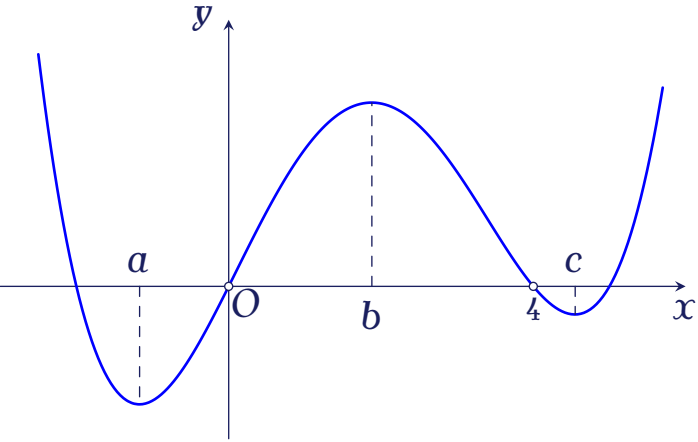
Dựa vào đồ thị \(y=f(x)\) ta thấy: $$f'(x)=0\Leftrightarrow\left[\begin{array}{ll}
x=a &\in\left(-\infty;0\right)\\
x=b &\in\left(0;4\right)\\
x=c &\in\left(4;+\infty\right)
\end{array}\right.$$
Ta có: \(g'(x)=\left(3x^2+6x\right)f'\left(x^3+3x^2\right)\).
Khi đó $\begin{aligned}[t]
g'(x)=0\Leftrightarrow&\left[\begin{array}{l}
3x^2+6x=0\\
f'\left(x^3+3x^2\right)=0
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{ll}
x=0\\ x=-2\\
x^3+3x^2=a &(1)\\
x^3+3x^2=b &(2)\\
x^3+3x^2=c &(3)
\end{array}\right.
\end{aligned}$
Xét hàm số \(h(x)=x^3+3x^2\) ta có \(h'(x)=3x^2+6x\).
Cho \(h'(x)=0\Leftrightarrow\left[\begin{array}{l}
x=0\\
x=-2.
\end{array}\right.\)

Dựa vào bảng biến thiên của \(h(x)\) ta thấy:
- Phương trình \((1)\) có \(1\) nghiệm.
- Phương trình \((2)\) có \(3\) nghiệm phân biệt.
- Phương trình \((3)\) có \(1\) nghiệm.
Vậy phương trình \(g'(x)=0\) có \(7\) nghiệm bội lẻ phân biệt nên \(g(x)\) có \(7\) điểm cực trị.
