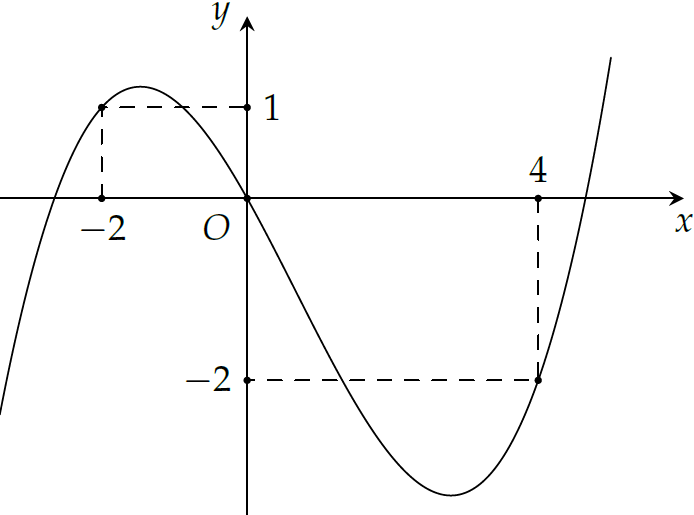
Cho hàm số \(f(x)\). Hàm số \(y=f'(x)\) có đồ thị như hình trên. Hàm số \(g(x)=f(1-2x)+x^2-x\) nghịch biến trên khoảng nào dưới đây?
| \(\left(1;\dfrac{3}{2}\right)\) | |
| \(\left(0;\dfrac{1}{2}\right)\) | |
| \(\left(-2;-1\right)\) | |
| \(\left(2;3\right)\) |
Chọn phương án A.
Ta có \(g'(x)=-2f'(1-2x)-(1-2x)\).
Khi đó $$\begin{aligned}
g'(x)\leq0\Leftrightarrow&-2f'(1-2x)-(1-2x)\leq0\\
\Leftrightarrow&f'(1-2x)\geq-\dfrac{1-2x}{2}\quad(1)
\end{aligned}$$
Đặt \(t=1-2x\), (1) trở thành \(\Leftrightarrow f'(t)\geq-\dfrac{t}{2}\).
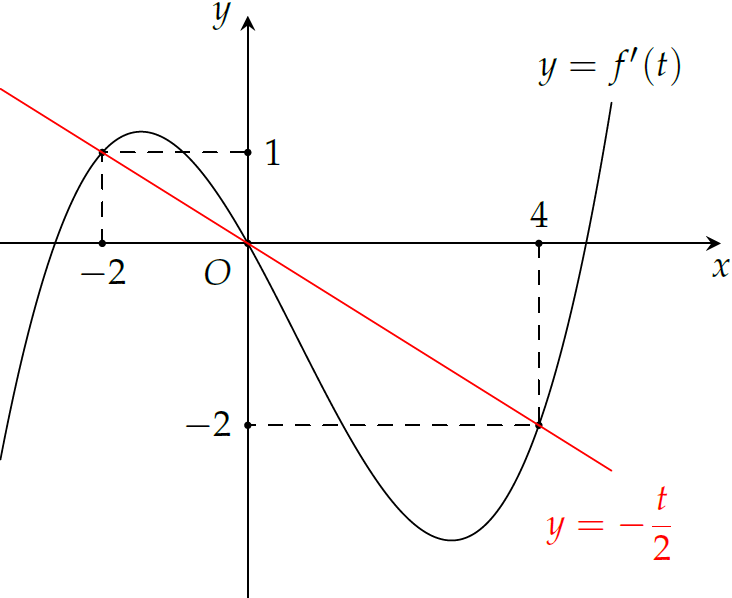
Quan sát đồ thị của \(y=f'(t)\) và \(y=-\dfrac{t}{2}\) ta thấy $$\begin{aligned}
f'(t)\geq-\dfrac{t}{2}\Leftrightarrow&\left[\begin{array}{l}
t\in[-2;0]\\
t\in[4;+\infty)
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
\begin{cases}
t\geq-2\\
t\leq0
\end{cases}\\
t\geq4
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
\begin{cases}
1-2x\geq-2\\
1-2x\leq0
\end{cases}\\
1-2x\geq4
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
\begin{cases}
x\leq\dfrac{3}{2}\\
x\geq\dfrac{1}{2}
\end{cases}\\
x\leq-\dfrac{3}{2}
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
x\in\left[\dfrac{1}{2};\dfrac{3}{2}\right]
x\in\left(-\infty;-\dfrac{3}{2}\right].
\end{array}\right.
\end{aligned}$$
Vậy \(g'(x)\leq0,\,\forall x\in\left(\dfrac{1}{2};\dfrac{3}{2}\right)\).
Suy ra \(g'(x)\leq0,\,\forall x\in\left(1;\dfrac{3}{2}\right)\).
Do đó, \(g(x)\) nghịch biến trên khoảng \(\left(1;\dfrac{3}{2}\right)\).
