Ngân hàng bài tập
A
Biết rằng tích phân \(\displaystyle\int\limits_{0}^{1}(2x+1)\mathrm{e}^x\mathrm{\,d}x=a+b\mathrm{e}\) với \(a,\,b\in\mathbb{Z}\). Tích \(ab\) bằng
| \(1\) | |
| \(-1\) | |
| \(-15\) | |
| \(20\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Gán giá trị \(\displaystyle\int\limits_{0}^{1}(2x+1)\mathrm{e}^x\mathrm{\,d}x\) cho biến nhớ A
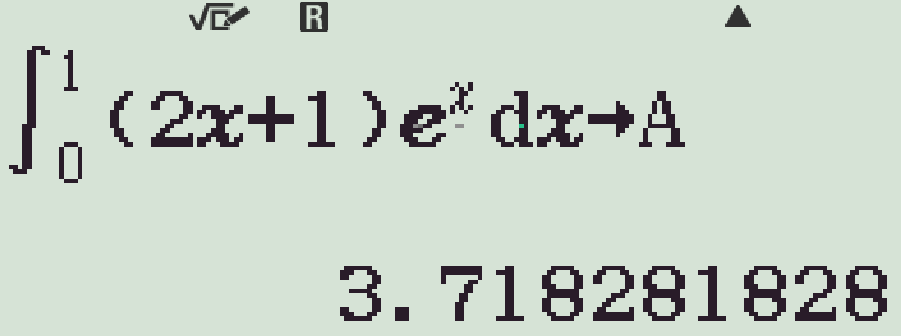
- Theo đó ta có \(a=f(b)=A-b\mathrm{e}\)
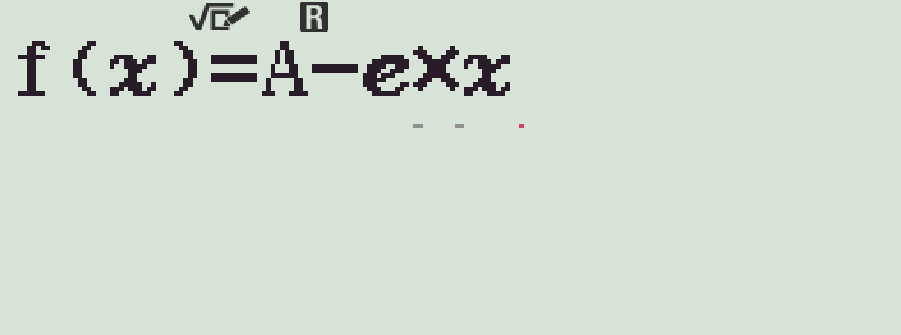
- Cho \(b\) biến thiên trên đoạn \([-10;10]\), bước nhảy bằng \(1\)
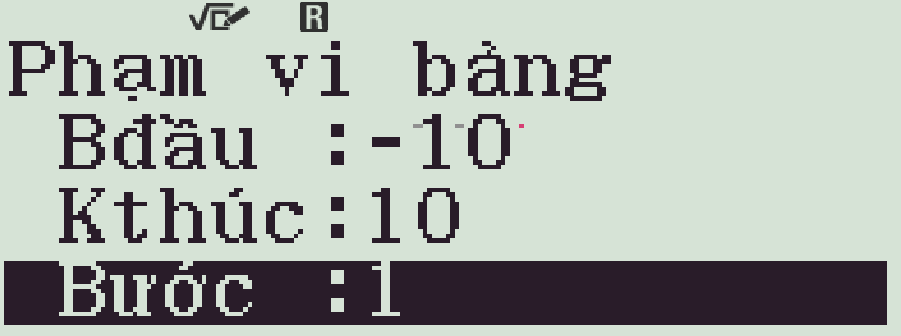
- Tìm giá trị \(x,\,y\) nguyên đủ nhỏ

Vậy \(a=b=1\). Suy ra \(ab=1\).
Chọn phương án A.
Đặt \(\begin{cases}
u=2x+1\\ v'=\mathrm{e}^x
\end{cases}\Leftrightarrow\begin{cases}
u'=2\\ v=\mathrm{e}^x.
\end{cases}\)
Khi đó $$\begin{aligned}
\displaystyle\int\limits_{0}^{1}(2x+1)\mathrm{e}^x\mathrm{\,d}x&=(2x+1)\mathrm{e}^x\bigg|_0^1-\displaystyle\int\limits_{0}^{1}2\mathrm{e}^x\mathrm{\,d}x\\
&=(3\mathrm{e}-1)-2\mathrm{e}^x\bigg|_0^1\\
&=(3\mathrm{e}-1)-(2\mathrm{e}-2)\\
&=1+\mathrm{e}.
\end{aligned}$$
Vậy \(a=b=1\).
Suy ra \(a\cdot b=1\).
