Ngân hàng bài tập
C
Tích phân \(I=\displaystyle\int\limits_{1}^{2}\left(x^2+\dfrac{x}{x+1}\right)\mathrm{\,d}x\) có giá trị là
| \(I=\dfrac{10}{3}+\ln2-\ln3\) | |
| \(I=\dfrac{10}{3}+\ln2+\ln3\) | |
| \(I=\dfrac{10}{3}-\ln2+\ln3\) | |
| \(I=\dfrac{10}{3}-\ln2-\ln3\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Tính tích phân đã cho
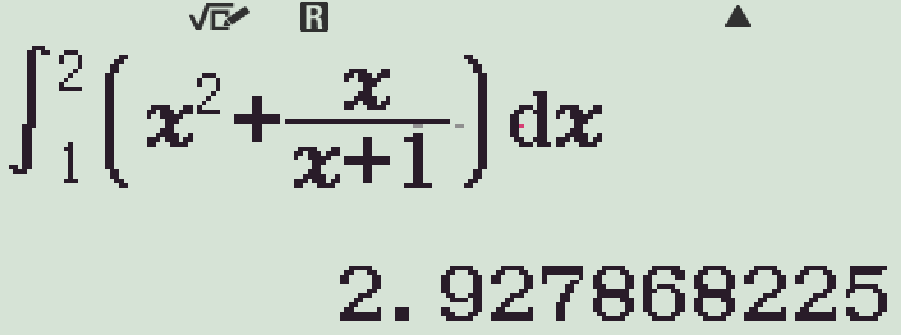
- Kiểm tra từng phương án
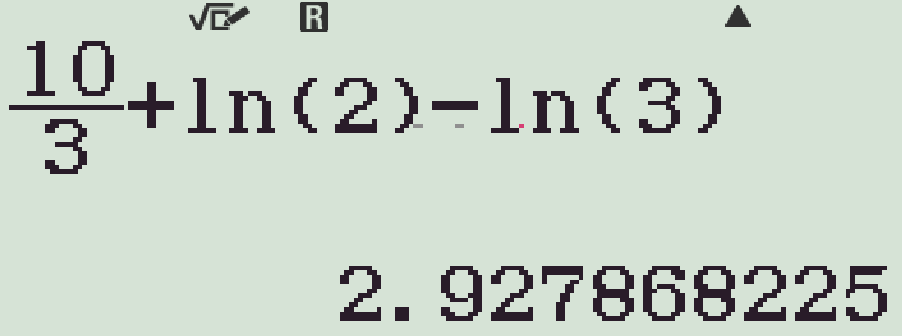
Vậy \(I=\dfrac{10}{3}+\ln2-\ln3\).
Chọn phương án A.
\(\begin{aligned}
I&=\displaystyle\int\limits_{1}^{2}\left(x^2+\dfrac{x}{x+1}\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_{1}^{2}\left(x^2+\dfrac{(x+1)-1}{x+1}\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_{1}^{2}\left(x^2+x-\dfrac{1}{x+1}\right)\mathrm{\,d}x\\
&=\left(\dfrac{x^3}{3}+\dfrac{x^2}{2}-\ln|x+1|\right)\bigg|_1^2\\
&=\dfrac{10}{3}+\ln2-\ln3.
\end{aligned}\)
