Ngân hàng bài tập
C
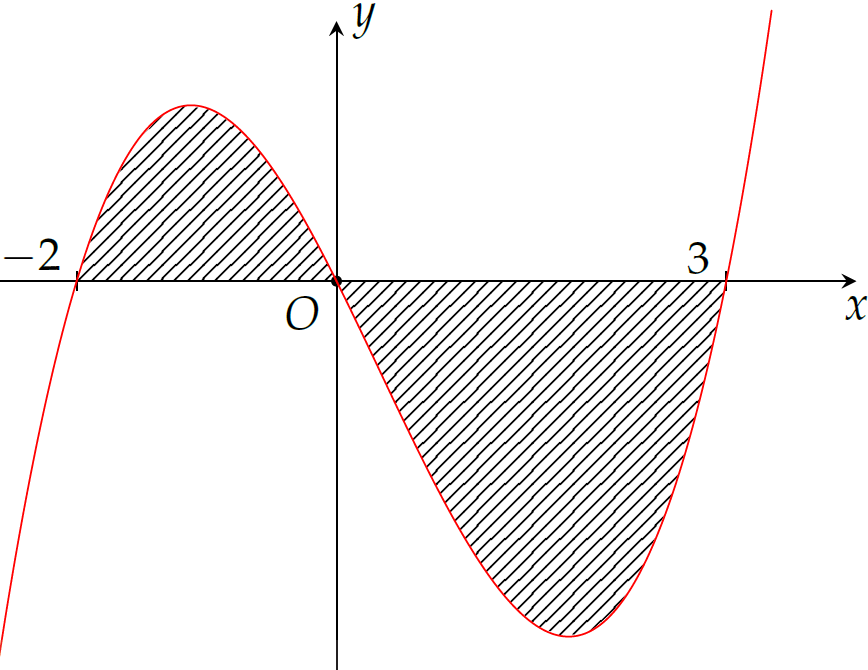
Cho đồ thị hàm số \(y=f(x)\) như hình vẽ và \(\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x=a\), \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=b\). Tính diện tích của phần được gạch chéo theo \(a\) và \(b\).
| \(\dfrac{a+b}{2}\) | |
| \(a-b\) | |
| \(b-a\) | |
| \(a+b\) |
1 lời giải
Chọn phương án B.
Theo hình vẽ ta có $$\begin{aligned}
S&=\displaystyle\int\limits_{-2}^{0}\left|f(x)\right|\mathrm{\,d}x+\displaystyle\int\limits_{0}^{3}\left|f(x)\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{3}\left(-f(x)\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x\\
&=a-b.
\end{aligned}$$
