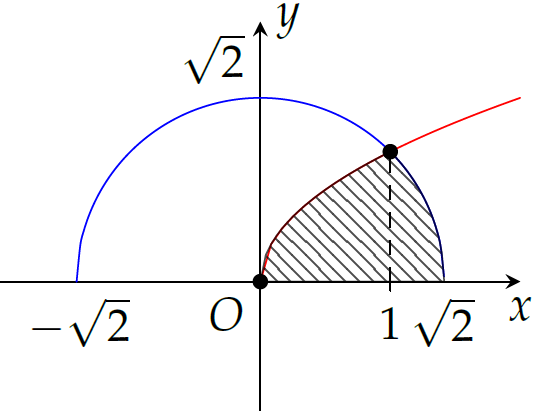
Cho \((H)\) là hình phẳng giới hạn bởi đường cong có phương trình \(y=\sqrt{x}\), nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) (với \(0\leq x\leq\sqrt{2}\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \((H)\) bằng
| \(\dfrac{3\pi+2}{12}\) | |
| \(\dfrac{4\pi+2}{12}\) | |
| \(\dfrac{3\pi+1}{12}\) | |
| \(\dfrac{4\pi+1}{6}\) |
Chọn phương án A.
Dùng máy tính cầm tay:
- Tính diện tích \(S\)
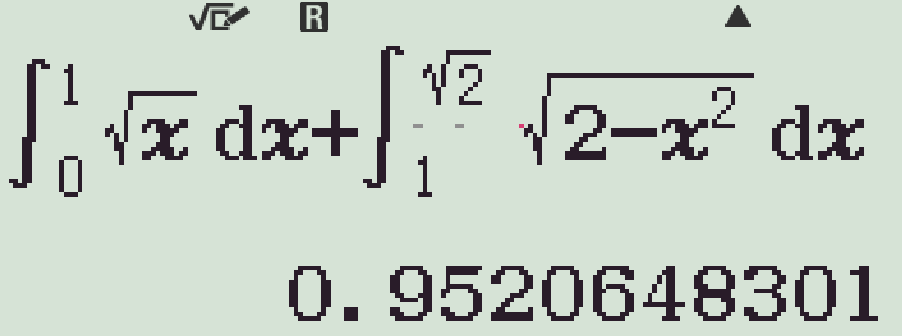
- Kiểm tra từng phương án

Vậy \(S=\dfrac{3\pi+2}{12}\).
Chọn phương án A.
Gọi \(S\) là diện tích của \((H)\). $$\begin{aligned}
S_1&=\displaystyle\int\limits_{0}^{1}\left(\sqrt{x}-0\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_{0}^{1}\sqrt{x}\mathrm{\,d}x\\
&=\displaystyle\int\limits_{0}^{1}x^{\tfrac{1}{2}}\mathrm{\,d}x\\
&=\dfrac{2}{3}\cdot x^{\tfrac{3}{2}}\bigg|_0^1=\dfrac{2}{3}.\quad(1)
\end{aligned}$$
Đặt \(x=\sqrt{2}\sin t\), với \(t\in\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\), ta có:
- \(\mathrm{\,d}x=\sqrt{2}\cos t\mathrm{\,d}t\)
- \(x=1\Rightarrow t=\dfrac{\pi}{4}\)
- \(x=\sqrt{2}\Rightarrow t=\dfrac{\pi}{2}\)
Khi đó $$\begin{aligned}
S_1&=\displaystyle\int\limits_{1}^{\sqrt{2}}\left(\sqrt{2-x^2}-0\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_{\tfrac{\pi}{4}}^{\tfrac{\pi}{2}}\sqrt{2-2\sin^2t}\cdot\sqrt{2}\cos t\mathrm{\,d}t\\
&=\displaystyle\int\limits_{\tfrac{\pi}{4}}^{\tfrac{\pi}{2}}\sqrt{2\cos^2t}\cdot\sqrt{2}\cos t\mathrm{\,d}t\\
&=\displaystyle\int\limits_{\tfrac{\pi}{4}}^{\tfrac{\pi}{2}}2\cos^2t\mathrm{\,d}t\\
&=\displaystyle\int\limits_{\tfrac{\pi}{4}}^{\tfrac{\pi}{2}}\left(1+\cos2t\right)\mathrm{\,d}t\\
&=\left(t+\dfrac{\sin2t}{2}\right)\bigg|_{\tfrac{\pi}{4}}^{\tfrac{\pi}{2}}\\
&=\dfrac{\pi-2}{4}.\quad(2)
\end{aligned}$$
Từ (1) và (2) suy ra \(S=S_1+S_2=\dfrac{2}{3}+\dfrac{\pi-2}{4}=\dfrac{3\pi+2}{12}\).
