Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y=|x|\) và \(y=x^2-2\).
| \(S=\dfrac{20}{3}\) | |
| \(S=\dfrac{11}{2}\) | |
| \(S=3\) | |
| \(S=\dfrac{13}{3}\) |
Chọn phương án A.
Phương trình hoành độ giao điểm: $$\begin{aligned}
|x|=x^2-2\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{l}
x=x^2-2\\
x=-x^2+2
\end{array}\right.
\end{cases}\\
\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{l}
x^2-x-2=0\\
x^2+x-2=0
\end{array}\right.
\end{cases}\\
\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{ll}
x=-1 &\text{(loại)}\\
x=2 &\text{(nhận)}\\
x=1 &\text{(loại)}\\
x=-2 &\text{(nhận)}
\end{array}\right.
\end{cases}
\end{aligned}$$
Vậy \(S=\displaystyle\int\limits_{-2}^{2}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x\).
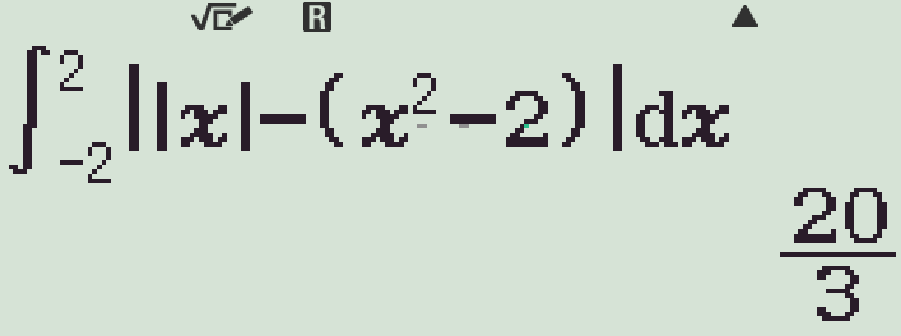
Chọn phương án A.
Phương trình hoành độ giao điểm: $$\begin{aligned}
|x|=x^2-2\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{l}
x=x^2-2\\
x=-x^2+2
\end{array}\right.
\end{cases}\\
\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{l}
x^2-x-2=0\\
x^2+x-2=0
\end{array}\right.
\end{cases}\\
\Leftrightarrow&\begin{cases}
x^2-2\geq0\\
\left[\begin{array}{ll}
x=-1 &\text{(loại)}\\
x=2 &\text{(nhận)}\\
x=1 &\text{(loại)}\\
x=-2 &\text{(nhận)}
\end{array}\right.
\end{cases}
\end{aligned}$$
Vậy \(S=\displaystyle\int\limits_{-2}^{2}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x\).
f(-x)&=|-x|-\left((-x)^2-2\right)\\
&=|x|-\left(x^2-2\right)\\
&=f(x).
\end{aligned}$$
Suy ra \(f(x)\) là hàm số chẵn.
Do đó $$\begin{aligned}
S&=\displaystyle\int\limits_{-2}^{2}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-2}^{0}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x+\displaystyle\int\limits_{0}^{2}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x\\
&=2\displaystyle\int\limits_{0}^{2}\left||x|-\left(x^2-2\right)\right|\mathrm{\,d}x\\
&=2\displaystyle\int\limits_{0}^{2}\left|x-\left(x^2-2\right)\right|\mathrm{\,d}x\\
&=2\displaystyle\int\limits_{0}^{2}\left|-x^2+x+2\right|\mathrm{\,d}x.
\end{aligned}$$
Bảng xét dấu:
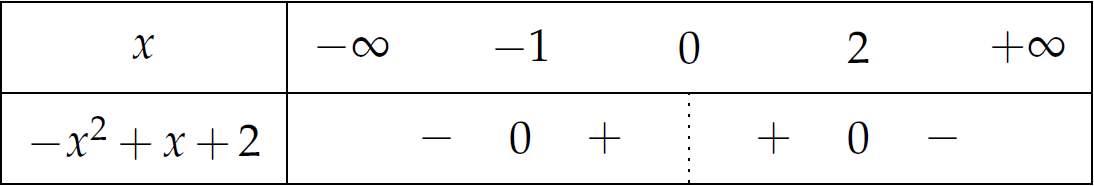
Theo đó $$\begin{aligned}
S&=2\displaystyle\int\limits_{0}^{2}\left|-x^2+x+2\right|\mathrm{\,d}x\\
&=2\displaystyle\int\limits_{0}^{2}\left(-x^2+x+2\right)\mathrm{\,d}x\\
&=2\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)\bigg|_0^2\\
&=\dfrac{20}{3}.
\end{aligned}$$
