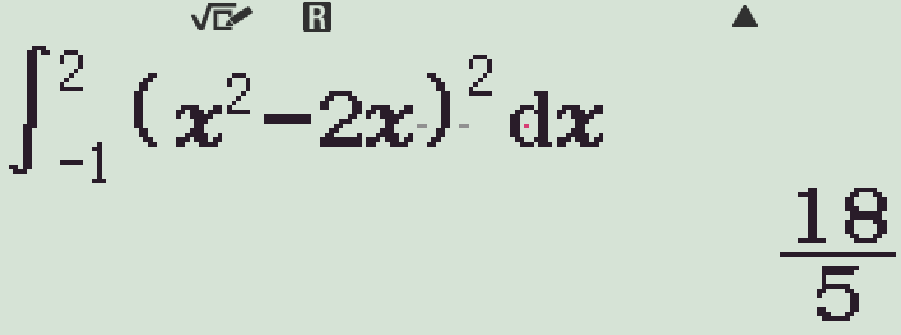Ngân hàng bài tập
C
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số \(y=x^2-2x\), \(y=0\), \(x=-1\), \(x=2\) quanh trục \(Ox\) bằng
| \(\dfrac{16\pi}{5}\) | |
| \(\dfrac{17\pi}{5}\) | |
| \(\dfrac{18\pi}{5}\) | |
| \(\dfrac{5\pi}{18}\) |
1 lời giải
Chọn phương án C.
\(\begin{aligned}
V&=\pi\displaystyle\int\limits_{-1}^{2}\left(x^2-2x\right)^2\mathrm{\,d}x\\
&=\pi\displaystyle\int\limits_{-1}^{2}\left(x^4-4x^3+4x^2\right)\mathrm{\,d}x\\
&=\pi\left(\dfrac{x^5}{5}-x^4+\dfrac{4x^3}{3}\right)\bigg|_{-1}^2\\
&=\dfrac{18\pi}{5}.
\end{aligned}\)