Ngân hàng bài tập
B
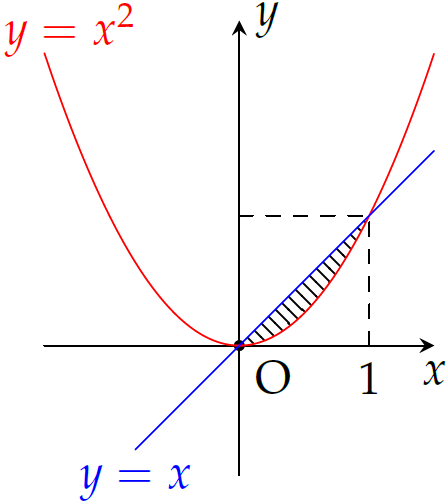
Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol \((P)\colon y=x^2\) và đường thẳng \(d\colon y=x\) xoay quanh trục \(Ox\) bằng
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x+\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)^2\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)\mathrm{\,d}x\) |
1 lời giải
Chọn phương án A.
Phương trình hoành độ giao điểm $$\begin{aligned}
x^2=x\Leftrightarrow&\,x^2-x=0\\
\Leftrightarrow\left[\begin{array}{l}
x=0\\
x=1.
\end{array}\right.
\end{aligned}$$
Xét dấu hàm số \(f(x)=x^2-x\) ta có

Vậy \(f(x)=x^2-x<0\) trên khoảng \((0;1)\), hay \(x^2< x\) với \(\forall x\in(0;1)\). Do đó $$V=\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x.$$