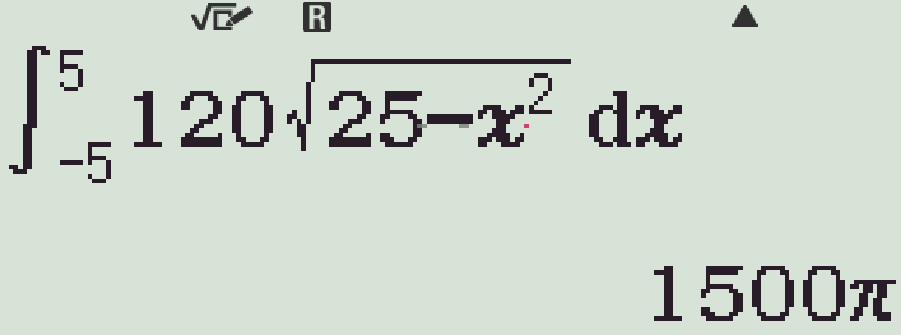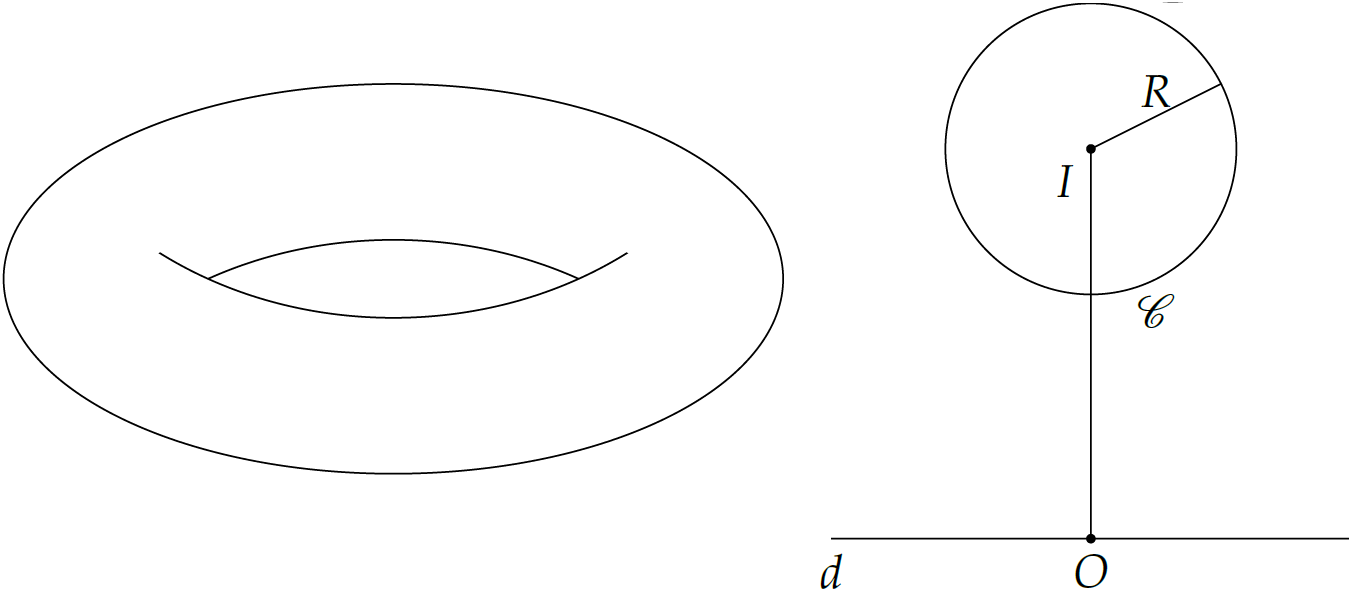
Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng cách quay đường tròn \(\mathscr{C}\) quanh trục \(d\)). Biết rằng \(OI=30\)cm, \(R=5\)cm. Tính thể tích \(V\) của chiếc phao.
| \(V=1500\pi^2\text{cm}^3\) | |
| \(V=9000\pi^2\text{cm}^3\) | |
| \(V=1500\pi\text{cm}^3\) | |
| \(V=9000\pi\text{cm}^3\) |
Chọn phương án A.
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
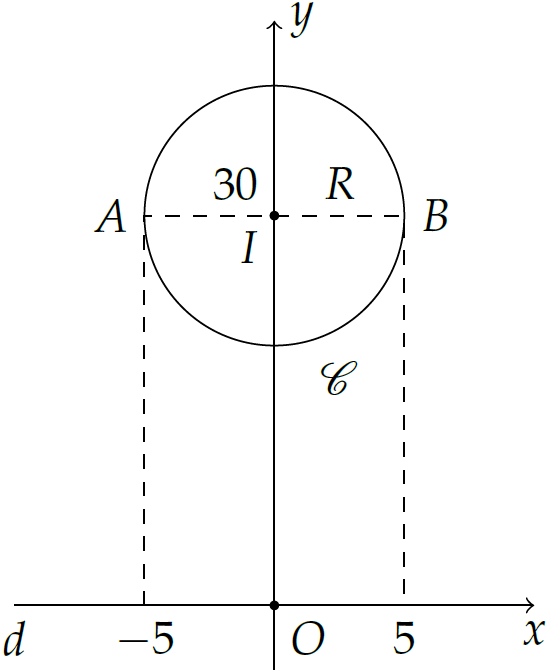
Khi đó, đường tròn \(\mathscr{C}\) có tâm \(I(0;30)\), bán kính \(R=5\) nên có phương trình là $$\begin{aligned}
x^2+(y-30)^2=25\Leftrightarrow&\,(y-30)^2=25-x^2\\
\Leftrightarrow&\left[\begin{array}{l}
y-30=\sqrt{25-x^2}\\
y-30=-\sqrt{25-x^2}
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
y=30+\sqrt{25-x^2}\\
y=30-\sqrt{25-x^2}.
\end{array}\right.
\end{aligned}$$
Khi đó $$\begin{aligned}
V&=\pi\displaystyle\int\limits_{-5}^{5}\left(30+\sqrt{25-x^2}\right)^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{-5}^{5}\left(30-\sqrt{25-x^2}\right)^2\mathrm{\,d}x\\
&=\pi\displaystyle\int\limits_{-5}^{5}120\sqrt{25-x^2}\mathrm{\,d}x.
\end{aligned}$$
Đặt \(t=5\sin t\), với \(t\in\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\), ta có:
- \(\mathrm{d}x=5\cos t\cdot\mathrm{\,d}t\)
- \(x=-5\Rightarrow t=-\dfrac{\pi}{2}\)
- \(x=5\Rightarrow t=\dfrac{\pi}{2}\)
Khi đó $$\begin{aligned}
V&=\pi\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}120\sqrt{25-25\sin^2t}\cdot5\cos t\mathrm{\,d}t\\
&=120\pi\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\sqrt{25\cos^2t}\cdot5\cos t\mathrm{\,d}t\\
&=120\pi\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}25\cos^2t\mathrm{\,d}t\\
&=3000\pi\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\dfrac{1+\cos2t}{2}\mathrm{\,d}t\\
&=1500\pi\displaystyle\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\left(1+\cos2t\right)\mathrm{\,d}t\\
&=1500\pi\left(t+\dfrac{\sin2t}{2}\right)\bigg|_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\\
&=1500\pi^2\text{cm}^3.
\end{aligned}$$