Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon x-y-z+6=0\) và \((Q)\colon2x+3y-2z+1=0\). Gọi \((S)\) là mặt cầu có tâm thuộc \((Q)\) và cắt \((P)\) theo giao tuyến là đường tròn tâm \(E(-1;2;3)\), bán kính \(r=8\). Phương trình mặt cầu \((S)\) là
| \(x^2+(y+1)^2+(z+2)^2=64\) | |
| \(x^2+(y-1)^2+(z-2)^2=67\) | |
| \(x^2+(y-1)^2+(z+2)^2=3\) | |
| \(x^2+(y+1)^2+(z-2)^2=64\) |
Chọn phương án B.
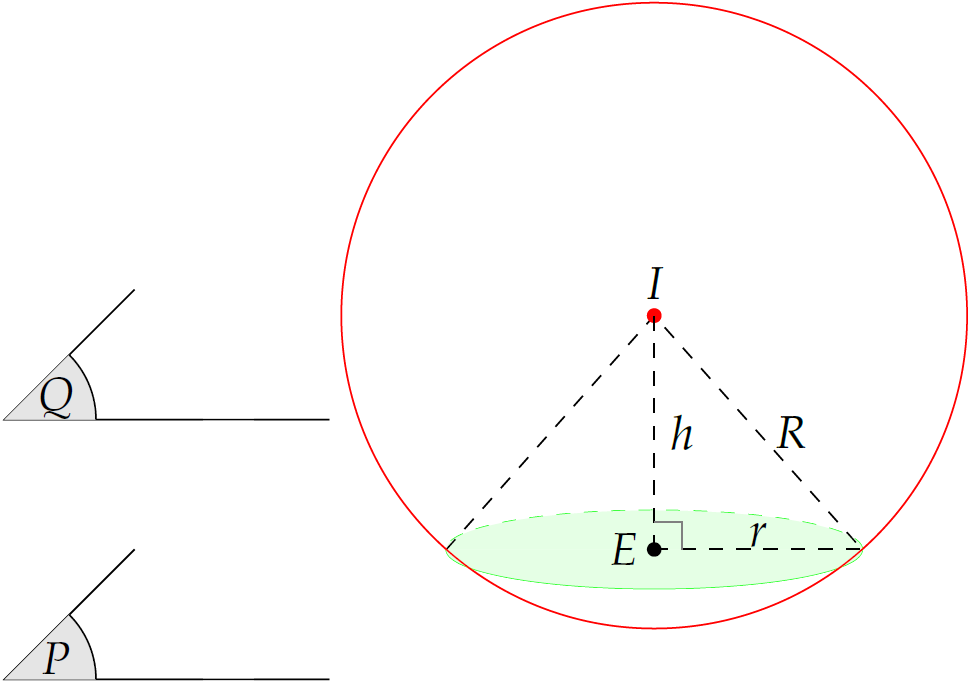
Giả sử \(I(x;y;z)\) là tâm của \((S)\).
Ta có:
- \(\overrightarrow{EI}=(x+1;y-2;z-3)\),
- \(\vec{n}=(1;-1;-1)\) là vectơ pháp tuyến của \((P)\).
Vì \((S)\) cắt \((P)\) theo giao tuyến là đường tròn tâm \(E\) nên suy ra \(IE\bot(P)\).
Do đó, \(\overrightarrow{IE}\) và \(\vec{n}\) cùng phương. Khi đó, tồn tại số thực \(t\) sao cho $$\begin{aligned}
\overrightarrow{EI}=t\cdot\vec{n}\Leftrightarrow&\begin{cases}
x+1&=t\\
y-2&=-t\\
z-3&=-t
\end{cases}\\
\Leftrightarrow&\begin{cases}
x=-1+t\\
y=2-t\\
z=3-t.
\end{cases}
\end{aligned}$$
Lại vì \(I\in(Q)\) nên ta có $$\begin{aligned}
&\,2(-1+t)+3(2-t)-2(3-t)+1=0\\
\Leftrightarrow&\,t-1=0\\
\Leftrightarrow&\,t=1.
\end{aligned}$$
Vậy \(I(0;1;2)\). (1)
Khi đó khoảng cách \(h\) từ tâm \(I\) đến mặt phẳng \((P)\) là $$\mathrm{d}\left(I,(P)\right)=\dfrac{|0-1-2+6|}{\sqrt{1^2+(-1)^2+(-1)^2}}=\sqrt{3}$$
Vậy bán kính của \((S)\) là $$R=\sqrt{r^2+h^2}=\sqrt{8^2+\sqrt{3}^2}=\sqrt{67}\quad(2)$$
Từ (1) và (2) suy ra $$(S)\colon x^2+(y-1)^2+(y-2)^2=67.$$
