Ngân hàng bài tập
A
Để phương trình \((m-1)x^2+3mx+m^2-m-6=0\) có hai nghiệm trái dấu thì
| \(m\in(-\infty;-2)\cup(1;3)\) | |
| \(m\in(-\infty;-2]\cup[1;3]\) | |
| \(m\in(-2;1)\cup(3;+\infty)\) | |
| \(m\in[-2;1]\cup[3;+\infty)\) |
1 lời giải
Chọn phương án A.
Để phương trình đã cho có hai nghiệm trái dấu thì $$a\cdot c<0\Leftrightarrow(m-1)\left(m^2-m-6\right)<0$$
- \(m-1=0\Leftrightarrow m=1\)
- \(m^2-m-6=0\Leftrightarrow\left[\begin{array}{l}m=-2\\ m=3\end{array}\right.\)
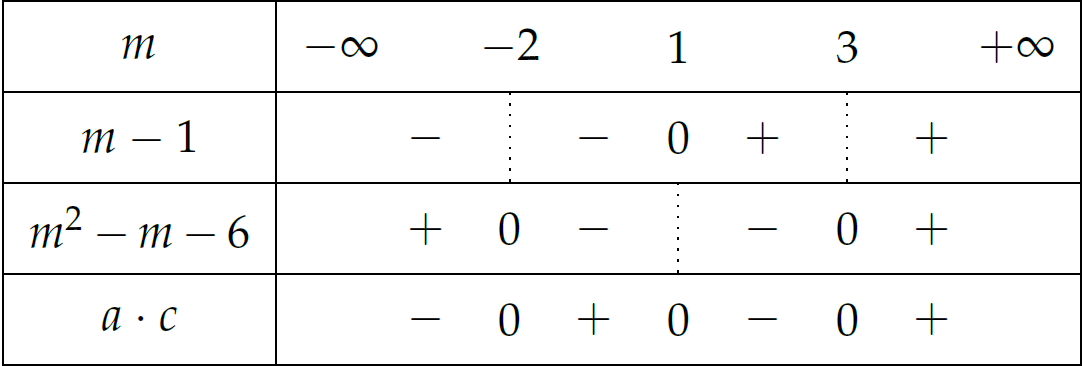
Suy ra \(m\in(-\infty;-2)\cup(1;3)\) thỏa mãn yêu cầu bài toán.
