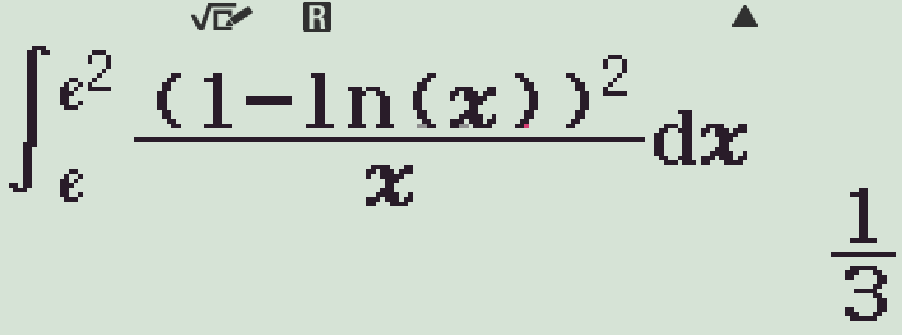Ngân hàng bài tập
C
Tính \(I=\displaystyle\int\limits_{\mathrm{e}}^{\mathrm{e}^2}\dfrac{\left(1-\ln x\right)^2}{x}\mathrm{\,d}x\) được kết quả là
| \(\dfrac{4}{3}\) | |
| \(\dfrac{5}{3}\) | |
| \(\dfrac{1}{3}\) | |
| \(\dfrac{13}{3}\) |
1 lời giải
Chọn phương án C.
Đặt \(u=\ln x\) ta có
- \(\mathrm{d}u=\dfrac{1}{x}\mathrm{\,d}x\)
- \(x=\mathrm{e}\Rightarrow u=\ln\mathrm{e}=1\)
- \(x=\mathrm{e}^2\Rightarrow u=\ln\mathrm{e}^2=2\)
Khi đó \(I=\displaystyle\int\limits_{1}^{2}(1-u)^2\mathrm{\,d}x=\dfrac{(1-u)^3}{3}\bigg|_1^2=\dfrac{1}{3}\).