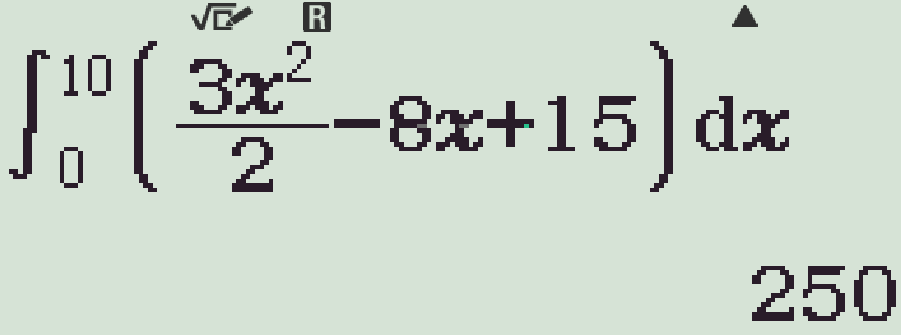Ngân hàng bài tập
A
Một ô tô đang chạy với vận tốc \(54\) km/h thì tăng tốc chuyển động nhanh dần đều với gia tốc \(a(t)=3t-8\) (m/s\(^2\)) trong đó \(t\) là khoảng thời gian tính bằng giây. Quãng đường mà ô tô đi được sau \(10\) s kể từ lúc tăng tốc là
| \(540\) m | |
| \(150\) m | |
| \(250\) m | |
| \(246\) m |
1 lời giải
Chọn phương án C.
Theo đề bài ta có $$\begin{aligned}
v(t)&=\displaystyle\int a(t)\mathrm{\,d}t\\
&=\displaystyle\int\left(3t-8\right)\mathrm{\,d}t=\dfrac{3t^2}{2}-8t+C.
\end{aligned}$$
Lúc chưa tăng tốc thì \(v(0)=54\text{ km/h}=\dfrac{54000}{3600}=15\text{ m/s}\). Do đó $$\dfrac{3\cdot0^2}{2}-8\cdot0+C=15\Leftrightarrow C=15$$Vậy \(v(t)=\dfrac{3t^2}{2}-8t+15\).
Vậy quãng đường ô tô đi được là $$\begin{aligned}
s&=\displaystyle\int\limits_{0}^{10}v(t)\mathrm{\,d}t\\
&=\displaystyle\int\limits_{0}^{10}\left(\dfrac{3t^2}{2}-8t+15\right)\mathrm{\,d}t\\
&=\left(\dfrac{t^3}{2}-4t^2+15t\right)\bigg|_0^{10}\\
&=250\text{ m}.
\end{aligned}$$