Cho số phức \(z=x+yi\) (\(x,\,y\in\mathbb{R}\)) có môđun nhỏ nhất thỏa mãn điều kiện \(|z-4-2i|=|z-2|\). Tính \(P=x^2+y^2\).
| \(10\) | |
| \(16\) | |
| \(8\) | |
| \(32\) |
Chọn phương án C.
- \(z-4-2i=(x-4)+(y-2)i\)
- \(z-2=(x-2)+yi\)
Theo đề bài ta có $$\begin{eqnarray*}
&|z-4-2i|&=|z-2|\\
\Leftrightarrow&\sqrt{(x-4)^2+(y-2)^2}&=\sqrt{(x-2)^2+y^2}\\
\Leftrightarrow&(x-4)^2+(y-2)^2&=(x-2)^2+y^2\\
\Leftrightarrow&-4x-4y+16&=0\\
\Leftrightarrow&x+y-4&=0.
\end{eqnarray*}$$
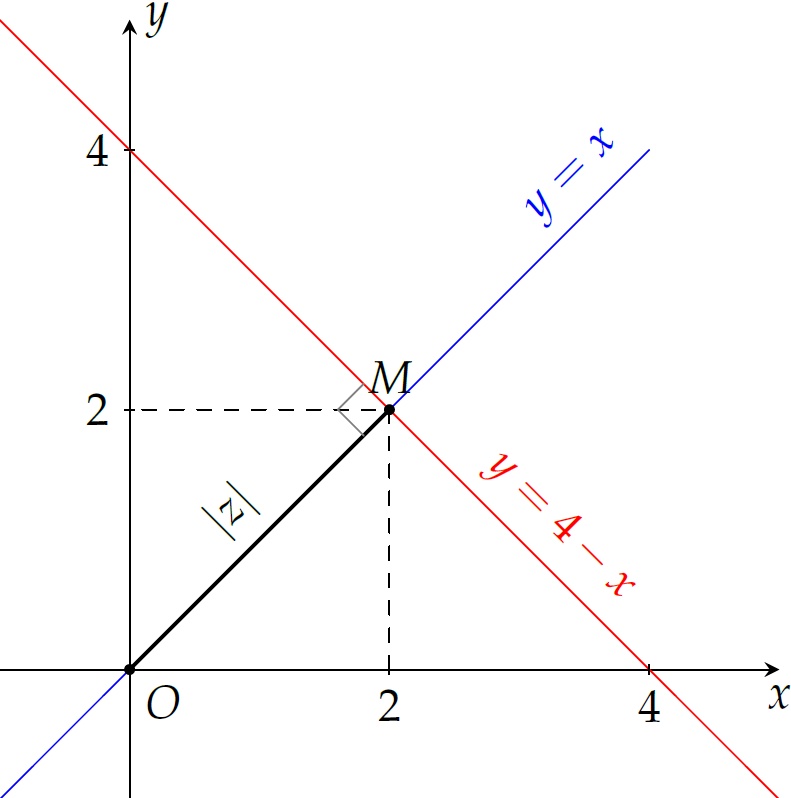
Vì \(|z|=OM\) nên \(|z|\) nhỏ nhất khi và chỉ khi \(OM\) ngắn nhất.
Khi đó, \(M\) là hình chiếu vuông góc của \(O\) trên đường thẳng \(\Delta\).
Gọi \(d\) là đường thẳng đi qua \(O\) và vuông góc với \(\Delta\). Khi đó \(d\cap\Delta=M\).
Vì \(d\bot\Delta\) nên \(\vec{n}\) là vectơ chỉ phương của \(\Delta\). Khi đó \(\vec{m}=(1;-1)\) là một vectơ pháp tuyến của \(d\). Do đó $$\begin{eqnarray*}
d\colon&(x-0)-(y-0)&=0\\
\Leftrightarrow&x-y&=0.
\end{eqnarray*}$$
Giải hệ phương trình \(\begin{cases}
x-y&=0\\
x+y-4&=0
\end{cases}\) ta được \(x=y=2\).
Vậy \(P=2^2+2^2=8\).
