Trong không gian \(Oxyz\), phương trình mặt cầu \((S)\) tiếp xúc với hai mặt phẳng song song \((P)\colon x-2y+2z+6=0\) và \((Q)\colon x-2y+2z-10=0\) có tâm \(I\) trên trục \(Oy\) là
| \(x^2+y^2+z^2+2y-\dfrac{55}{9}=0\) | |
| \(x^2+y^2+z^2+2y-60=0\) | |
| \(x^2+y^2+z^2-2y+55=0\) | |
| \(x^2+y^2+z^2-2y-\dfrac{55}{9}\) |
Chọn phương án A.
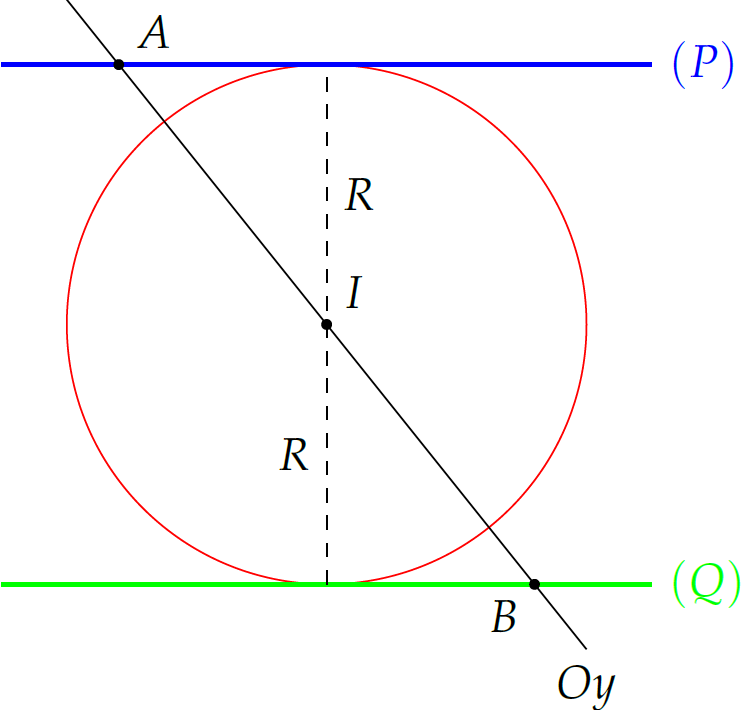
Gọi \(A,\,B\) lần lượt là giao điểm của \(Oy\) với \((P),\,(Q)\). Ta có
- \(0-2y+2\cdot0+6=0\Rightarrow y=3\Rightarrow A(0;3;0)\)
- \(0-2y+2\cdot0-10=0\Rightarrow y=-5\Rightarrow B(0;-5;0)\)
Suy ra \(I(0;-1;0)\).
Khi đó \(R=\mathrm{d}\left(I,(P)\right)=\dfrac{|-2\cdot(-1)+6|}{3}=\dfrac{8}{3}\).
Vậy mặt cầu \((S)\) có phương trình $$\begin{aligned}
(x-0)^2+(y+1)^2+(z-0)^2&=\dfrac{64}{9}\\
\Leftrightarrow\,x^2+y^2+z^2+2y-\dfrac{55}{9}&=0.
\end{aligned}$$
Chọn phương án A.
Giả sử \(I(0;y;0)\in Oy\). Ta có $$\begin{aligned}
&\mathrm{d}\left(I,(P)\right)=\mathrm{d}\left(I,(Q)\right)\\
\Leftrightarrow&\dfrac{|-2y+6|}{3}=\dfrac{|-2y-10|}{3}\\
\Leftrightarrow&\dfrac{|-2y+6|}{3}=\dfrac{|-2y-10|}{3}\\
\Leftrightarrow&\left[\begin{array}{l}-2y+6=-2y-10\\ -2y+6=2y+10\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{ll}6=-10 &\text{(loại)}\\ y=-1\end{array}\right.
\end{aligned}$$
Vậy \(I(0;-1;0)\).
Khi đó \(R=\mathrm{d}\left(I,(P)\right)=\dfrac{|-2\cdot(-1)+6|}{3}=\dfrac{8}{3}\).
Vậy mặt cầu \((S)\) có phương trình $$\begin{aligned}
(x-0)^2+(y+1)^2+(z-0)^2&=\dfrac{64}{9}\\
\Leftrightarrow\,x^2+y^2+z^2+2y-\dfrac{55}{9}&=0.
\end{aligned}$$
