Ngân hàng bài tập
B
Cho tích phân \(\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x\) và đặt \(t=\sqrt{1+x}\). Mệnh đề nào sau đây đúng?
| \(\displaystyle\int\limits_{1}^{2}\left(t^2-1\right)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{1}^{2}\left(2t^2+2t\right)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{1}^{2}\left(t^2+t\right)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{1}^{2}\left(2t^2-2t\right)\mathrm{\,d}t\) |
2 lời giải
Chọn phương án D.
Dùng máy tính cầm tay:
- Tính \(\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x\).
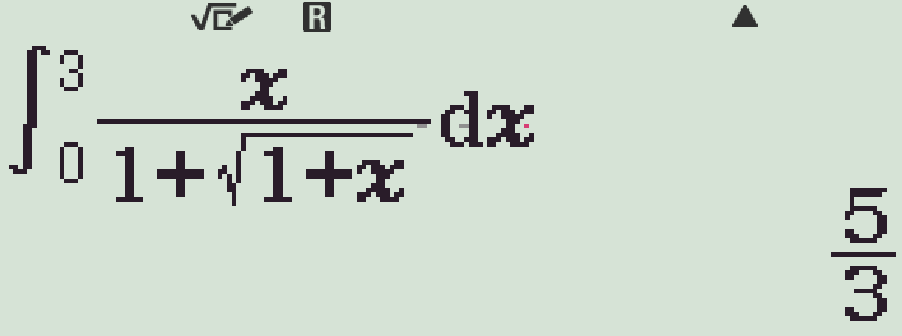
- Lần lượt kiểm tra các phương án, ta có
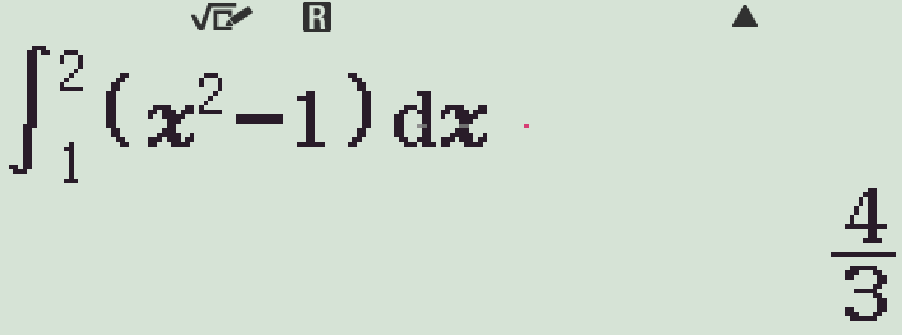
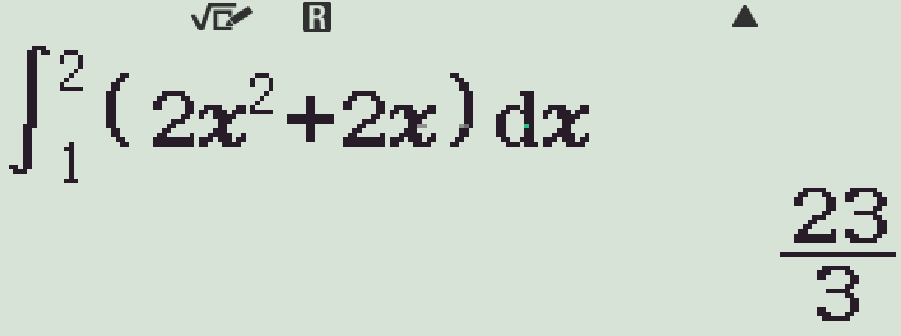
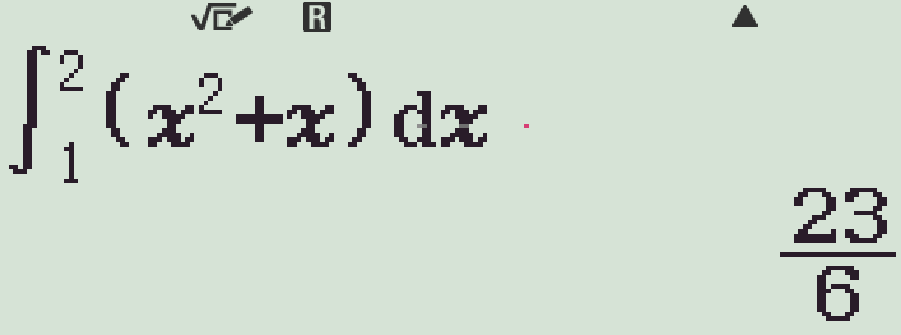
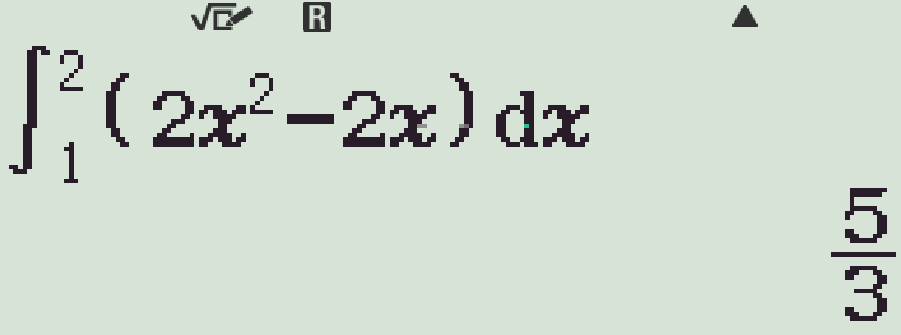
Vậy \(\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x=\displaystyle\int\limits_{1}^{2}\left(2t^2-2t\right)\mathrm{\,d}t\).
Chọn phương án D.
Với \(t=\sqrt{1+x}\) ta có
- \(t^2=1+x\Rightarrow x=t^2-1\Rightarrow\mathrm{\,d}x=2t\mathrm{\,d}t\)
- \(x=0\Rightarrow t=\sqrt{1+0}=1\)
- \(x=3\Rightarrow t=\sqrt{1+3}=2\)
Khi đó $$\begin{aligned}
\displaystyle\int\limits_{0}^{3}\dfrac{x}{1+\sqrt{1+x}}\mathrm{\,d}x&=\displaystyle\int\limits_{1}^{2}\dfrac{t^2-1}{1+t}\cdot2t\mathrm{\,d}t\\
&=\displaystyle\int\limits_{1}^{2}\dfrac{(t+1)(t-1)}{1+t}\cdot2t\mathrm{\,d}t\\
&=\displaystyle\int\limits_{1}^{2}2t(t-1)\mathrm{\,d}t\\
&=\displaystyle\int\limits_{1}^{2}\left(2t^2-2t\right)\mathrm{\,d}t.
\end{aligned}$$
