Ngân hàng bài tập
A
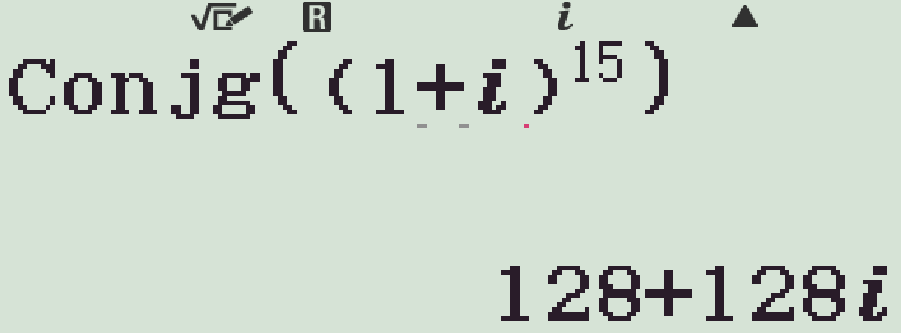
Số phức liên hợp của số phức \(z=(1+i)^{15}\) là
| \(\overline{z}=128+128i\) | |
| \(\overline{z}=128-128i\) | |
| \(\overline{z}=-1\) | |
| \(\overline{z}=-128-128i\) |
1 lời giải
Chọn phương án A.
- \((1+i)^2=2i\)
- \((1+i)^3=2i(1+i)=-2+2i\)
- \((1+i)^4=(2i)^2=-4\)
Khi đó ta có $$\begin{aligned}
z&=(1+i)^{12}\cdot(1+i)^3\\
&=\left[(1+i)^4\right]^3\cdot(-2+2i)\\
&=(-4)^3(-2+2i)\\
&=128-128i.
\end{aligned}$$
Vậy \(\overline{z}=128+128i\).