Ngân hàng bài tập
B
Tập nghiệm của bất phương trình \(\sqrt{2}x^2-\left(1+\sqrt{2}\right)x+1<0\) là
| \(\left(\dfrac{\sqrt{2}}{2};1\right)\) | |
| \(\varnothing\) | |
| \(\left[\dfrac{\sqrt{2}}{2};1\right]\) | |
| \(\left(-\infty;\dfrac{\sqrt{2}}{2}\right)\cup(1;+\infty)\) |
1 lời giải
Chọn phương án A.
\(\sqrt{2}x^2-\left(1+\sqrt{2}\right)x+1=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=\dfrac{\sqrt{2}}{2}.\end{array}\right.\)
Bảng xét dấu: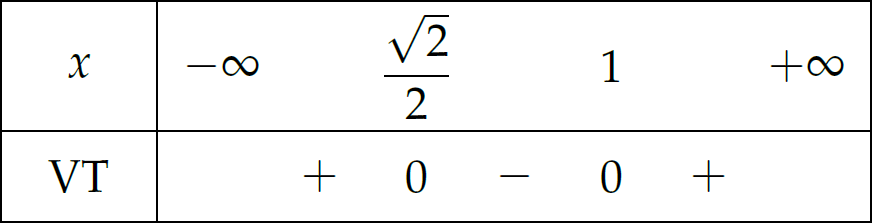
Theo đó, \(S=\left(\dfrac{\sqrt{2}}{2};1\right)\).
