Ngân hàng bài tập
A
Giải bất phương trình $$x(x+5)\leq2\left(x^2+2\right)$$
| \(S=(-\infty;1]\) | |
| \(S=[1;4]\) | |
| \(S=(-\infty;1]\cup[4;+\infty)\) | |
| \(S=[4;+\infty)\) |
1 lời giải
Chọn phương án C.
\(\begin{eqnarray*}
&x(x+5)&\leq2\left(x^2+2\right)\\
\Leftrightarrow&x^2+5x&\leq2x^2+4\\
\Leftrightarrow&x^2-5x+4&\geq0.
\end{eqnarray*}\)
\(x^2-5x+4=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=4.\end{array}\right.\)
Bảng xét dấu: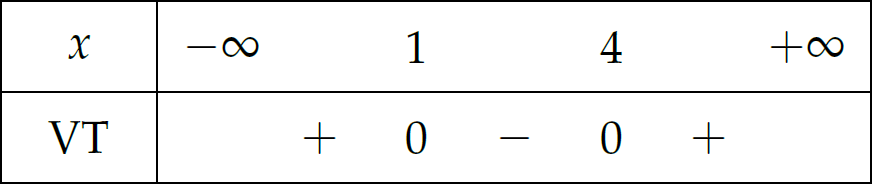
Theo đó, \(S=(-\infty;1]\cup[4;+\infty)\).
