Ngân hàng bài tập
S
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn $$\dfrac{x+3}{x^2-4}-\dfrac{1}{x+2}<\dfrac{2x}{2x-x^2}?$$
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
1 lời giải
Chọn phương án C.
\(\begin{eqnarray*}
&\dfrac{x+3}{x^2-4}-\dfrac{1}{x+2}&<\dfrac{2x}{2x-x^2}\\
\Leftrightarrow&\dfrac{x+3}{(x-2)(x+2)}-\dfrac{1}{x+2}&<\dfrac{2x}{-x(x-2)}\\
\Leftrightarrow&\dfrac{x+3}{(x-2)(x+2)}-\dfrac{1}{x+2}+\dfrac{2x}{x(x-2)}&<0\\
\Leftrightarrow&\dfrac{x(x+3)-x(x-2)+2x(x+2)}{x(x-2)(x+2)}&<0\\
\Leftrightarrow&\dfrac{2x^2+9x}{\left(x^2-2x\right)(x+2)}&<0\\
\end{eqnarray*}\)
- \(2x^2+9x=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=-\dfrac{9}{2}.\end{array}\right.\)
- \(x^2-2x=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=2.\end{array}\right.\)
- \(x+2=0\Leftrightarrow x=-2\)
Bảng xét dấu: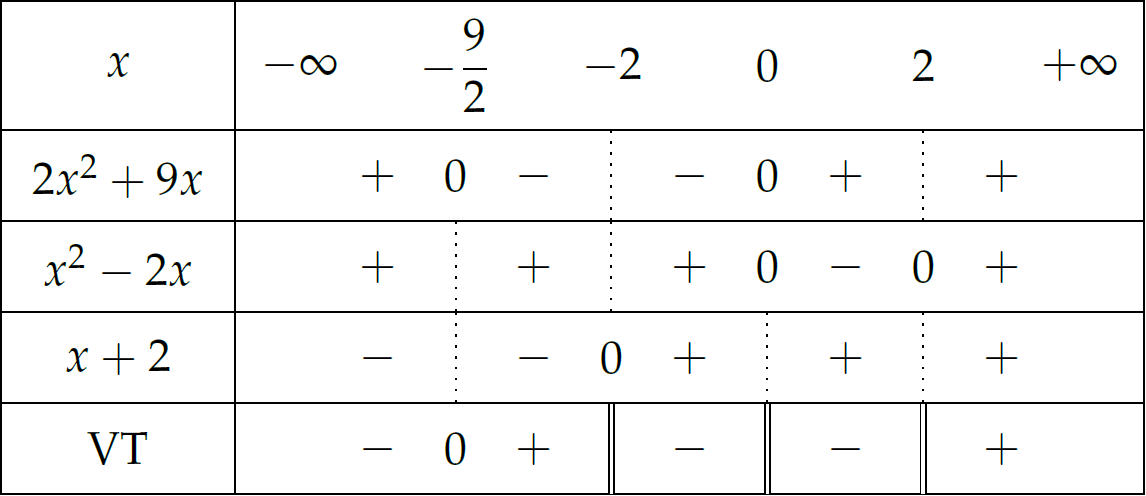
Suy ra \(S=\left(-\infty;-\dfrac{9}{2}\right)\cup(-2;0)\cup(0;2)\).
Do đó, chỉ có \(1\) giá trị nguyên dương thỏa đề là \(x=1\).
