Ngân hàng bài tập
A
Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\sqrt{2x^2-5x+2}$$
| \(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\) | |
| \(\mathscr{D}=\left[2;+\infty\right)\) | |
| \(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\cup[2;+\infty)\) | |
| \(\mathscr{D}=\left[\dfrac{1}{2};2\right]\) |
1 lời giải
Chọn phương án C.
Điều kiện xác định: \(2x^2-5x+2\geq0\).
Bảng xét dấu: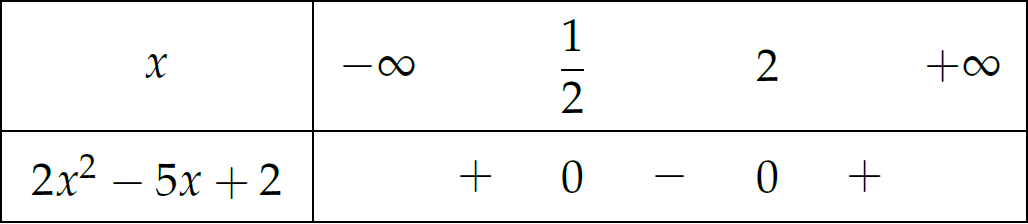
Suy ra \(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\cup[2;+\infty)\).
