Ngân hàng bài tập
S
Số giá trị nguyên của tham số \(m\) để hàm số $$y=x^3-(m+2)x^2+\left(m^2+2m\right)x$$có cực trị là
| \(2\) | |
| \(1\) | |
| \(3\) | |
| \(0\) |
1 lời giải
Chọn phương án A.
\(y'=3x^2-2(m+2)x+m^2+2m\).
Hàm số đã cho là hàm đa thức bậc ba, có cực trị khi phương trình \(y'=0\) có \(2\) nghiệm phân biệt, tức là $$\begin{aligned}
\Delta'>0\Leftrightarrow&\,(m+2)^2-3\left(m^2+2m\right)>0\\
\Leftrightarrow&\,m^2+4m+4-3m^2-6m>0\\
\Leftrightarrow&\,-2m^2-2m+4>0\\
\Leftrightarrow&\,m^2+m-2<0.
\end{aligned}$$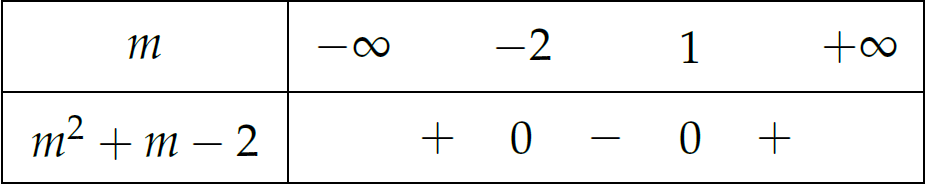
Vậy \(m\in(-2;1)\).
Do đó, có \(2\) giá trị nguyên của \(m\) thỏa đề là \(m=-1\) và \(m=0\).
